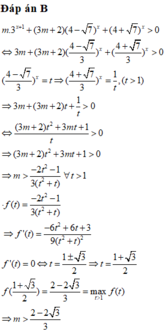Tìm m để bất phương trình x³ - x² + (m - 2)x + m 0 nghiệm đúng với mọi x > 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


3:
x^2-2x+1-m^2<=0
=>(x-1)^2-m^2<=0
=>(x-1)^2<=m^2
=>-m<=x-1<=m
=>-m+1<=x<=m+1
mà x thuộc [-1;2]
nên -m+1>=-1 và m+1<=2
=>-m>=-2 và m<=1
=>m<=2 và m<=1
=>m<=1

1.
\(\Leftrightarrow\left\{{}\begin{matrix}m< 0\\\Delta=\left(m+1\right)^2-4m\left(m-1\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 0\\-3m^2+7m+1< 0\end{matrix}\right.\)
\(\Leftrightarrow m< \dfrac{7-\sqrt{61}}{6}\)
2.
\(\Leftrightarrow\left\{{}\begin{matrix}m>0\\\Delta'=4\left(m+1\right)^2-m\left(m-5\right)\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>0\\3m^2+13m+4\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>0\\-4\le m\le-\dfrac{1}{3}\end{matrix}\right.\)
Không tồn tại m thỏa mãn

\(\int_{\Delta'=\left(m+1\right)^2-3\left(m-1\right)\left(m-2\right)<0}^{m-1>0}\)\(\int\limits^{m>1}_{-2m^2-7m+-5<0}\)=>\(\int_{m<-1;m>\frac{5}{2}}^{m>1}\)=> m > 5/2

Với m=−1m=−1 thì PT f(x)=0f(x)=0 có nghiệm x=1x=1 (chọn)
Với m≠−1m≠−1 thì f(x)f(x) là đa thức bậc 2 ẩn xx
f(x)=0f(x)=0 có nghiệm khi mà Δ′=m2−2m(m+1)≥0Δ′=m2−2m(m+1)≥0
⇔−m2−2m≥0⇔m(m+2)≤0⇔−m2−2m≥0⇔m(m+2)≤0
⇔−2≤m≤0⇔−2≤m≤0
Tóm lại để f(x)=0f(x)=0 có nghiệm thì m∈[−2;0]

Để phương trình có nghiệm đúng với mọi x thì
(2m)^2-4(m-2)(-m-2)<0 và m-2<0
=>4m^2+4(m^2-4)<0 và m<2
=>8m^2-16<0 và m<2
=>m^2<2
=>-căn 2<m<căn 2