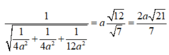Chi tứ diện ABCD , tam giác ABC và ACD cân tại A và B; M là trung điểm của CD.
a) Cm (ACD) ⊥(BCD)
b) Kẻ MH⊥BM chứng minh AH⊥(BCD)
c) Kẻ HK⊥(AM), cm HK⊥(ACD)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
7 tháng 8 2017
Tương tự 2B. Ta chứng minh được ABCD là hình thang vuông. Từ đó tính được diện tích ABCD là:
S A B C D = s A B C + s A C D = 1 2 A C . A B + 1 2 C A . D H = 1 2 .4.4 + 1 2 .4.2 = 12 c m 2
(Với DH là đường cao tam giác ACD)
B1
13 tháng 9 2017
(1-->27 đâu rồi)
28.
AB=AD = BC => ABC cân
=> góc BAC = BCA
mà BCA= ACD (so le)
=> BCA= ACD
=> CA là tia phân giác góc c
..dpcm...
29.là hình thang cân
xét 2 tam giác AOC,BOD
đây là 2 tam giác cân ,chung có số đo góc đỉnh A = nhau (đđ)
=> 2 tam giac đồng dạng
=> góc C= góc D => AC\\ DC (2 góc so le = nhau)
lại có AB = CD => nó cân (2 đg chéo = nhau)
30.
a. hình thang cân
2 tam giác cân ADE ~ ABC => D=E => DE\\ BC (đồng vị)
BD= AB-AD = AC-AE = EC
b.
như trên đã cm DE = BD=EC => EB là tia phân giác goc B
=> E,D là chân đg phân giác hạ từ B,C đến AC,AB
CM
9 tháng 5 2017
Đáp án là B.
B C = A B 2 = 2 a 2 .Gọi H là trung điểm BC ta có:
A H ⊥ B C B C = A B C ∩ D B C A B C ⊥ D B C ⇒ A H ⊥ D B C
kẻ H E ⊥ D C , H K ⊥ A E (1)
D C ⊥ H E D C ⊥ A H ( d o A H ⊥ D B C ⊂ D C ) ⇒ D C ⊥ A H E ⇒ D C ⊥ H K 2
từ 1 & 2 H K ⊥ A D C ⇒ d H ; A D C = H K
d B ; A D C = 2 d H ; A D C = 2 A H . H E A H 2 + H E 2 = 2 6 3
A H = B C 2 , H E = A B 2 ; A H = B C 2 = a 2 , H E = B C 2 = a
17 tháng 8 2021
Tổng số phần của 2 diện tích tam giác :
3 + 2 =5 ( phần )
Diện tích tam giác ACD :
70 : 5 x 3 = 52 ( cm2)
Diện tích tam giác ABC :
70 : 5 x 2 = 28 ( cm2)
Vậy : diện tích tam giác ACD : 52 cm2
______________ ABC : 28 cm2
CM
25 tháng 8 2017
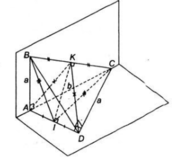
Chứng minh tương tự, ta có tam giác AKD là tam giác cân tại K có KI là đường trung tuyến nên đồng thời là đường cao.
⇒ IK ⊥ AD (2)
Từ (1) và (2) suy ra; IK là đường vuông góc chung của hai đường thẳng AD và BC.
CM
8 tháng 3 2018
Đáp án A
Chọn hệ trục tọa độ Oxy
A D = 2 a tan 60 o = 2 a 3
Từ M kẻ MH song song với AC ta có MH =a
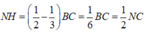
PT của mặt phẳng (BCD) là x 2 a + y 2 a + z 2 3 a = 1
Vậy khoảng cách từ
P
(
0
;
4
a
;
0
)
đến (BCD) là:
