Cho tam giác ABC có A(0;3), B(3;2), C(2;4). Tìm tâm đường tròn ngoại tiếp tam giác ABC.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
11 tháng 10 2019
Ta có: AB → = (−a; b; 0) và AC → = (−a; 0; c)
Vì AB → . AC → = a 2 > 0 nên góc ∠ BAC là góc nhọn.
Lập luận tương tự ta chứng minh được các góc ∠ B và ∠ C cũng là góc nhọn.
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
a) Do \(\widehat{A}=100^0>90^0\) nên là góc tù, do đó, \(\widehat{A}\) là góc lớn nhất trong tam giác ABC.
\( \Rightarrow \) BC là cạnh lớn nhất của tam giác ABC (do BC đối diện với góc A trong tam giác ABC)
b)
Theo định lí tổng 3 góc trong tam giác ABC, ta có:
\( \Rightarrow \widehat A + \widehat B + \widehat C = {180^o}\)
\( \Rightarrow \widehat C = {180^o} - {100^o} - {40^o} = {40^o}\)
\( \Rightarrow\widehat C = \widehat B = {40^o}\)
\( \Rightarrow \) ABC là tam giác cân tại A.
14 tháng 1 2021
Tọa độ trọng tâm G của ΔABC là \(G\left(1;\dfrac{m}{3}\right)\)
⇒ \(\left\{{}\begin{matrix}\overrightarrow{AG}=\left(2;\dfrac{m}{3}\right)\\\overrightarrow{BG}=\left(-3;\dfrac{m}{3}\right)\end{matrix}\right.\)
Để ΔGAB vuông tại G
⇒ GA ⊥ GB
⇒ \(\overrightarrow{GA}\) ⊥ \(\overrightarrow{GB}\)
⇒ \(\overrightarrow{GA}.\overrightarrow{GB}=0\)
⇒ 2 . (-3) + \(\dfrac{m^2}{9}\) = 0
⇒ m2 = 6 . 9 = 54
⇒ m = \(\pm\sqrt{54}\)
Mình chắc chắn cách làm của mình là đúng còn về tính toán thì chưa chắc nên bạn tự kiểm tra nhá 
CM
8 tháng 11 2018
Gọi tọa độ điểm H(a;b)
Ta có: A H → = a + 1 ; b − 1 , B H → = a ; b − 2 , B C → = 1 ; − 1 , A C → 2 ; 0
Do H là trực tâm tam giác ABC nên:
A C → . B H → = 0 B C → . A H → = 0 ⇒ 2. a + 0. b − 2 = 0 1. a + 1 − 1. b − 1 = 0 ⇒ a = 0 b = 2
Vậy H (0; 2).
Chọn A
21 tháng 6 2021
Ta có: \(AC^2+BC^2=\left(a\sqrt{2}\right)^2+\left(a\sqrt{3}\right)^2=2a^2+3a^2=5a^2\)
\(AB^2=\left(a\sqrt{5}\right)^2=5a^2\)
=> \(AB^2=AC^2+BC^2\)
=> Tam giác ABC vuông tại C (định lí Pytago đảo)
CM
29 tháng 6 2018
Chọn B.
Ta có:
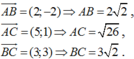
Mặt khác 
Suy ra diện tích tam giác ABC là 1/2.AB.BC = 6.
CM
6 tháng 10 2018
Ta có:
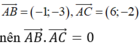
Suy ra tam giác ABC vuông tại A do đó trực tâm H trùng với A
Vậy H( -1 ; 3)
Chọn B.
Gọi đường tròn ngoại tiếp tam giác là
\(\left(C\right):x^2+y^2-2ax-2by+c=0\). Khi đó tâm đường tròn ngoại tiếp tam giác ABC là \(I\left(a,b\right)\)
Ta có: \(A\left(0,3\right)\in\left(C\right)\Rightarrow9-6b+c=0\Rightarrow-6b+c=-9\)
\(B\left(3,2\right)\in\left(C\right)\Rightarrow9+4-6a-4b+c=0\Rightarrow-6a-4b+c=-13\)
\(C\left(2;4\right)\in\left(C\right)\Rightarrow4+16-4a-8b+c=0\Rightarrow-4a-8b+c=-20\)
Ta có hệ: \(\left\{{}\begin{matrix}-6b+c=-9\\-6a-4b+c=-13\\-4a-8b+c=-20\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a=\dfrac{3}{2}\\b=\dfrac{5}{2}\\c=6\end{matrix}\right.\)
Vậy tọa độ tâm đường tròn ngoại tiếp tam giác ABC là \(I\left(\dfrac{3}{2};\dfrac{5}{2}\right)\)