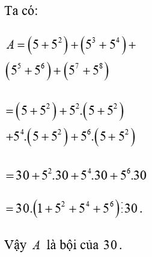Chứng minh
A = 5+52+53.....58 là bội của 30
B = 3+33+35....+329 là bội của 9
Nhanh lên nha
Mình cần gấp
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
PG
0
Những câu hỏi liên quan
CM
27 tháng 10 2017
a, A = 5 + 5 2 + 5 3 + . . . + 5 8
= 5(1+5)+ 5 2 (1+5)+ 5 3 (1+5)+...+ 5 7 (1+5)
= 30+5.30+ 5 2 .30+...+ 5 6 .30
= 30.(1+5+ 5 2 +..+ 5 6 )
Vậy A là bội của 30
b, B = 3 + 3 3 + 3 5 + 3 7 + . . . + 3 29
= 3 1 + 3 2 + 3 4 + 3 7 1 + 3 2 + 3 4 +...+ 3 27 1 + 3 2 + 3 4
= 273+273. 3 6 +...+ 3 26 .273
= 273.(1+ 3 6 +...+ 3 26 )
Vậy B là bội của 273
CC
1
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
18 tháng 8 2023
A = 5 + 52 + 53 +...+ 58
A = (5 + 52) +( 53 + 54) +...+ ( 57 + 58)
A = 30 + 52.(5 + 52) +...+ 56.(5 + 52)
A = 30.( 1 + 52 +...+ 56) (đpcm)
PT
1
CM
9 tháng 12 2019
Ta có: A = 5 + 5 2 + 5 3 + 5 4 + 5 5 + 5 6 + 5 7 + 5 8
= 5 + 5 2 + 5 2 5 + 5 2 + 5 4 5 + 5 2 + 5 6 5 + 5 2
= 30 + 5 2 . 30 + 5 4 . 30 + 5 6 . 30
= 30 . ( 1 + 5 2 + 5 4 + 5 6 ) ⋮ 30
Vậy A là bội của 30
PT
1
M
1
28 tháng 1 2018
=> -A = 5^59-5^58+5^57-5^56+.....+5-1
Nhóm 4 số thành 1 nhóm thì sẽ có 15 nhóm mà mỗi nhóm đều chia hết cho 52
Ví dụ : 5^59-5^58+5^57+5^56 = 5^56.(5^3-5^2+5-1) = 5^56.104 = 2.52.5^56 chia hết cho 52
=> -A chia hết cho 52
=> A chia hết cho 52
=> đpcm
Tk mk nha
5 tháng 2 2022
a) \(A=\left(5+5^2\right)+5^2\left(5+5^2\right)+...+5^6\left(5+5^2\right)=30+5^2.30+...+5^6.30\)
\(=30\left(1+5^2+...+5^6\right)⋮30\Rightarrowđpcm\)
b) \(B=\left(3+3^3+3^5\right)+3^6\left(3+3^3+3^5\right)+...+3^{24}\left(3+3^3+3^5\right)=273+3^6.273+...+3^{24}.273\)
\(=273.\left(1+3^6+...+3^{24}\right)⋮273\Rightarrowđpcm\)
5 tháng 2 2022
a: \(B=5\left(1+5+5^2+5^3\right)+5^5\left(1+5+5^2+5^3\right)\)
\(=156\cdot5\cdot\left(1+5^4\right)\)
\(=780\left(1+5^4\right)⋮30\)
b: \(B=\left(3+3^3+3^5\right)+...+3^{24}\left(3+3^2+3^5\right)\)
\(=273\cdot\left(1+...+3^{24}\right)⋮273\)
PN
0
AH
Akai Haruma
Giáo viên
13 tháng 12 2021
Lời giải:
$A=(5-5^2)-(5^3+5^4)-(5^5+5^6)$
$=5(1-5)-5^4(1+5)-5^5(1+5)$
$=-20-5^4.6-5^5.6=-20-30.5^3-30.5^4$
$=-20-30(5^3+5^4)$ không chia hết cho $30$ cho $20$ không chia hết cho $30$
Do đó $A$ không thể là bội của $30$