cho x = \(\sqrt{3+\sqrt{5}}\)và y= \(\sqrt{3-\sqrt{5}}\)
tính A= x.y và B = x-y
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
ST
Song Toàn Võ
4 tháng 5 2022
Đúng(0)
Những câu hỏi liên quan
28 tháng 9 2021
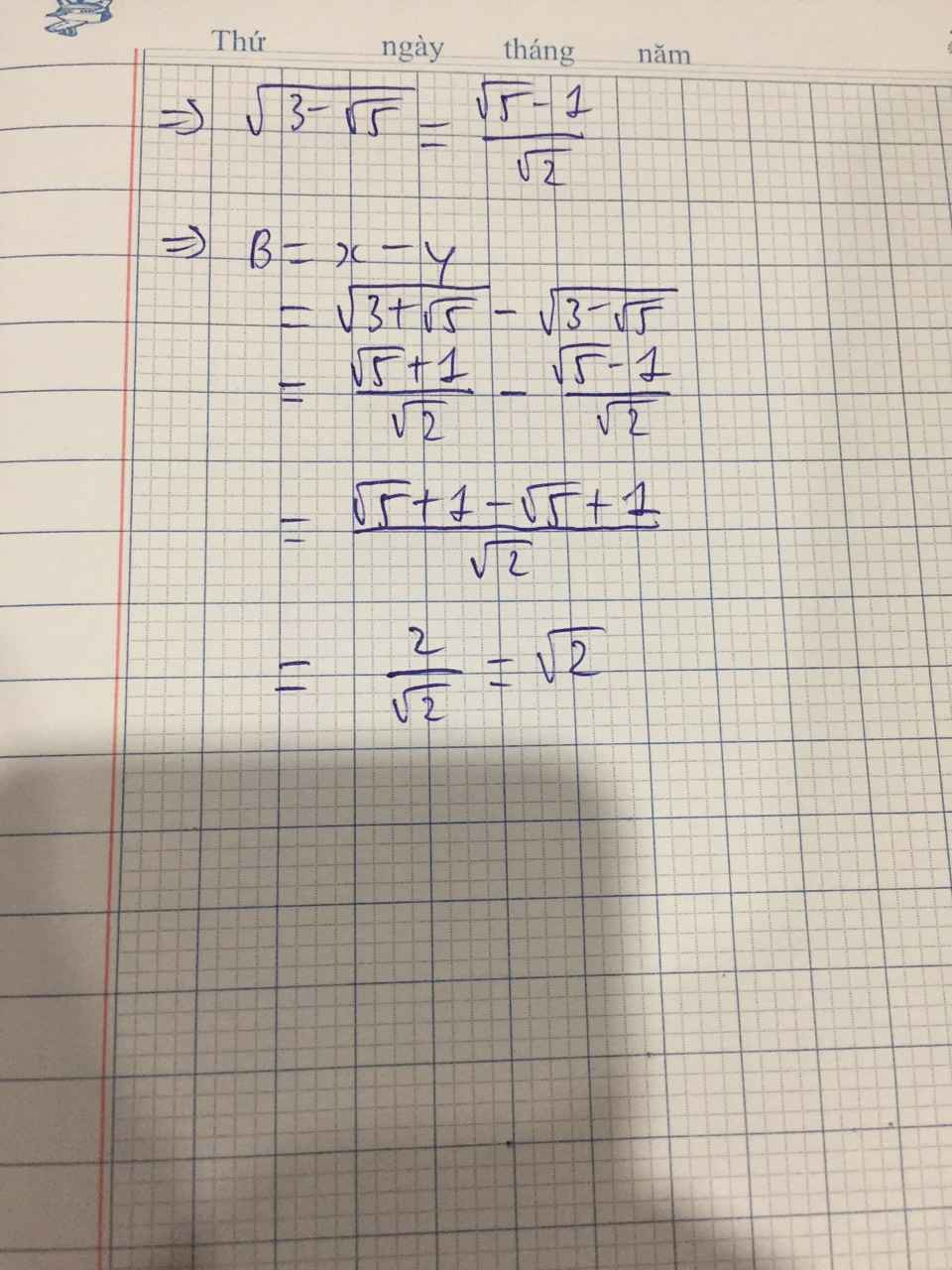
\(x=\sqrt[3]{9+4\sqrt{5}}+\sqrt[3]{9-4\sqrt{5}}\\ \Leftrightarrow x^3=9+4\sqrt{5}+9-4\sqrt{5}+3\sqrt[3]{\left(9-4\sqrt{5}\right)\left(9+4\sqrt{5}\right)}\left(\sqrt[3]{9+4\sqrt{5}}+\sqrt[3]{9-4\sqrt{5}}\right)\\ \Leftrightarrow x^3=18+3x\sqrt[3]{81-80}=18-3x\\ \Leftrightarrow x^3-3x=18\\ y=\sqrt[3]{3-2\sqrt{2}}+\sqrt[3]{3+2\sqrt{2}}\\ \Leftrightarrow y^3=6+3\sqrt[3]{\left(3-2\sqrt{2}\right)\left(3+2\sqrt{2}\right)}\left(\sqrt[3]{3-2\sqrt{2}}+\sqrt[3]{3+2\sqrt{2}}\right)\\ \Leftrightarrow y^3=6+3y\sqrt[3]{9-8}=6+3y\\ \Leftrightarrow y^3-3y=6\\ \Leftrightarrow P=x^3+y^3-3\left(x+y\right)+1993\\ P=x^3+y^3-3x-3y+1993=18+6+1993=2017\)
28 tháng 9 2021
Áp dụng: \(\left(a+b\right)^3=a^3+3a^2b+3ab^2+b^3=a^3+b^3+3ab\left(a+b\right)\)
\(x=\sqrt[3]{9+4\sqrt{5}}+\sqrt[3]{9-4\sqrt{5}}\)
\(\Rightarrow x^3=9+4\sqrt{5}+9-4\sqrt{5}+3\sqrt[3]{\left(9+4\sqrt{5}\right)\left(9-4\sqrt{5}\right)}\left(\sqrt[3]{9+4\sqrt{5}}+\sqrt[3]{9-4\sqrt{5}}\right)\)
\(=18+3\sqrt[3]{81-80}.x=18+3x\)
\(y=\sqrt[3]{3-2\sqrt{2}}+\sqrt[3]{3+2\sqrt{2}}\)
\(\Rightarrow y^3=3-2\sqrt{2}+3+2\sqrt{2}+3\sqrt[3]{\left(3-2\sqrt{2}\right)\left(3+2\sqrt{2}\right)}\left(\sqrt[3]{3-2\sqrt{2}}+\sqrt[3]{3+2\sqrt{2}}\right)\)
\(=6+3\sqrt[3]{9-8}y=6+3y\)
\(P=x^3+y^3-3\left(x+y\right)+1993\)
\(=18+3x+6+3y-3x-3y+1993=2017\)
26 tháng 8 2021
\(A=\dfrac{x\sqrt{x}+y\sqrt{y}}{\sqrt{x}+\sqrt{y}}=x-\sqrt{xy}+y\)
\(B=\dfrac{\sqrt{x}-\sqrt{y}}{x\sqrt{x}-y\sqrt{y}}=\dfrac{1}{x+\sqrt{xy}+y}\)
\(C=\dfrac{3\sqrt{3}+x\sqrt{x}}{3-\sqrt{3x}+x}=\sqrt{x}+\sqrt{3}\)
\(D=\dfrac{x+\sqrt{5x}+5}{x\sqrt{x}-5\sqrt{5}}=\dfrac{1}{\sqrt{x}-\sqrt{5}}\)
CV
4 tháng 7 2019
Bài 2 xét x=0 => A =0
xét x>0 thì \(A=\frac{1}{x-2+\frac{2}{\sqrt{x}}}\)
để A nguyên thì \(x-2+\frac{2}{\sqrt{x}}\inƯ\left(1\right)\)
=>cho \(x-2+\frac{2}{\sqrt{x}}\)bằng 1 và -1 rồi giải ra =>x=?
4 tháng 7 2019
1,Ta có \(\left(\sqrt{a}+\sqrt{b}+\sqrt{c}\right)^2=a+b+c+2\sqrt{ab}+2\sqrt{bc}+2\sqrt{ac}\)
=> \(\sqrt{ab}+\sqrt{bc}+\sqrt{ac}=2\)
\(a+2=a+\sqrt{ab}+\sqrt{bc}+\sqrt{ac}=\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}+\sqrt{c}\right)\)
\(b+2=\left(\sqrt{b}+\sqrt{c}\right)\left(\sqrt{b}+\sqrt{a}\right)\)
\(c+2=\left(\sqrt{c}+\sqrt{b}\right)\left(\sqrt{c}+\sqrt{a}\right)\)
=> \(\frac{\sqrt{a}}{a+2}+\frac{\sqrt{b}}{b+2}+\frac{\sqrt{c}}{c+2}=\frac{\sqrt{a}}{\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}+\sqrt{c}\right)}+\frac{\sqrt{b}}{\left(\sqrt{b}+\sqrt{c}\right)\left(\sqrt{b}+\sqrt{a}\right)}+...\)
=> \(\frac{\sqrt{a}}{a+2}+...=\frac{2\left(\sqrt{ab}+\sqrt{bc}+\sqrt{ac}\right)}{\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}+\sqrt{c}\right)\left(\sqrt{b}+\sqrt{c}\right)}=\frac{4}{\sqrt{\left(a+2\right)\left(b+2\right)\left(c+2\right)}}\)
=> M=0
Vậy M=0
AT
20 tháng 6 2021
a) ĐKXĐ: \(x,y\ge0\)
\(M=\dfrac{x\sqrt{y}-\sqrt{y}-y\sqrt{x}+\sqrt{x}}{1+\sqrt{xy}}=\dfrac{x\sqrt{y}-y\sqrt{x}+\sqrt{x}-\sqrt{y}}{1+\sqrt{xy}}\)
\(=\dfrac{\sqrt{xy}\left(\sqrt{x}-\sqrt{y}\right)+\left(\sqrt{x}-\sqrt{y}\right)}{1+\sqrt{xy}}=\dfrac{\left(\sqrt{x}-\sqrt{y}\right)\left(1+\sqrt{xy}\right)}{1+\sqrt{xy}}=\sqrt{x}-\sqrt{y}\)
b) \(x=\left(1-\sqrt{3}\right)^2\Rightarrow\sqrt{x}=\sqrt{\left(1-\sqrt{3}\right)^2}=\left|1-\sqrt{3}\right|=\sqrt{3}-1\)
\(y=3-\sqrt{8}\Rightarrow\sqrt{y}=\sqrt{3-\sqrt{8}}=\sqrt{3-2\sqrt{2}}=\sqrt{\left(\sqrt{2}\right)^2-2.\sqrt{2}.1+1^2}\)
\(=\sqrt{\left(\sqrt{2}-1\right)^2}=\left|\sqrt{2}-1\right|=\sqrt{2}-1\)
\(\Rightarrow M=\left(\sqrt{3}-1\right)-\left(\sqrt{2}-1\right)=\sqrt{3}-\sqrt{2}\)
G
2
4 tháng 12 2015
Thay dấu thôi
A3 =10 -9A
A3 +9A -10 =0
=> A =1 ; A = -10 loại
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 1 2021
\(x=\dfrac{1}{\sqrt{2}}\left(\sqrt{4+2\sqrt{3}}+\sqrt{4-2\sqrt{3}}\right)\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{\left(\sqrt{3}+1\right)^2}+\sqrt{\left(\sqrt{3}-1\right)^2}\right)=\sqrt{6}\)
\(y=\sqrt{\left(\sqrt{6}-1\right)^2}=\sqrt{6}-1\)
\(\Rightarrow x-y=1\Rightarrow P=1\)
\(B=x-2020-\sqrt{x-2020}+\dfrac{1}{4}+\dfrac{8079}{4}\)
\(B=\left(\sqrt{x-2020}-\dfrac{1}{2}\right)^2+\dfrac{8079}{4}\ge\dfrac{8079}{4}\)
\(B_{min}=\dfrac{8079}{4}\) khi \(x=\dfrac{8081}{4}\)