cho a,b,m khác 0 thỏa mãn a+b+m=0 tính (1+a/b)×(1+b/m)×(1+m/a) Xin mn giúp mik với ạ mik sắp thi rùi😓😓😓
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A= x2-20x+101
= x2-20x+100+1
= (x2-20x+100)+1
= (x-10)2+1
do (x-10)2 ≥ 0 ∀ x
⇔ (x-10)2+1 ≥ 1 ∀ x
⇔ A ≥ 1 ∀ x
=> min A =1 khi x=10
B= x2-4xy+5y2+10x-22y+28
= (x2-4xy+4y2)+ (10x+20y) +25+(y2+2y+1)+2
= [(x-2y)2+10(x-2y)+25]+(y+1)2+2
= (x-2y+5)2+(y+1)2+2
do (x-2y+5)2 ≥ 0∀ x;y
(y+1)2 ≥ 0∀ y
=> (x-2y+5)2 + (y+1)2 ≥ 0∀ x;y
⇔ (x-2y+5)2+(y+1)2+2 ≥ 2∀ x;y
⇔ B ≥ 2∀ x;y
min B =2 khi y=-1;x=-3


Phương trình hoành độ giao điểm (d) và (P):
\(x^2-2x-3=ax-a-3\)
\(\Leftrightarrow x^2-\left(a+2\right)x+a=0\)
\(\Delta=\left(a+2\right)^2-4a=a^2+4>0;\forall a\Rightarrow\) (d) luôn cắt (P) tại 2 điểm pb
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_A+x_B=a+2\\x_Ax_B=a\end{matrix}\right.\)
Mặt khác do A, B thuộc (d) nên: \(\left\{{}\begin{matrix}y_A=ax_A-a-3\\y_B=ax_B-a-3\end{matrix}\right.\)
\(y_A+y_B=0\)
\(\Leftrightarrow a\left(x_A+x_B\right)-2a-6=0\)
\(\Leftrightarrow a\left(a+2\right)-2a-6=0\)
\(\Leftrightarrow a^2-6=0\)
\(\Leftrightarrow a=\pm\sqrt{6}\)

a, X x 9,9 + X : 10 = 12,5
X x 9,9 + X x 0,1 = 12,5
X x (9,9 + 0,1) = 12,5
X x 10 = 12,5
X = 12,5 : 10 = 1,25
---
X + X : 2 + X : 4 + X : 8 = 37,725
X : (1 + 2 + 4 + 8) = 37,725
X : 15 = 37,725
X = 37,725 x 15 = 565,875
a; \(x\) \(\times\) 9,9 + \(x\) : 10 = 12,5
\(x\) \(\times\) 9,9 + \(x\) \(\times\) 0,1 = 12,5
\(x\) \(\times\) (9,9 + 0,1) = 12,5
\(x\) \(\times\) 10 = 12,5
\(x\) = 12,5 : 10
\(x\) = 1,25
b; \(x\) + \(x\) : 2 + \(x\) : 4 + \(x\) : 8 = 37,725
\(x\) \(\times\) 1 + \(x\) \(\times\) \(\dfrac{1}{2}\) + \(x\) \(\times\) \(\dfrac{1}{4}\) + \(x\) \(\times\) \(\dfrac{1}{8}\)= 37,725
\(x\) \(\times\)(1 + \(\dfrac{1}{2}\) + \(\dfrac{1}{4}\) + \(\dfrac{1}{8}\)) = 37,725
\(x\) \(\times\) \(\dfrac{15}{8}\) = 37,725
\(x\) = 37,725 : \(\dfrac{15}{8}\)
\(x\) = 20,12

k) 10 (24-3x):15=250-244
10(24-3x):15=6
10(24-3x)=6.15
10(24-3x)=90
24-3x=90:10
24-3x=9
3x=24-9
3x=15
x=15:3=5


\(\left(2x+1\right)^2-\frac{4}{9}=0\)
\(\Leftrightarrow\left(2x+1\right)^2=\frac{4}{9}\)
\(\Leftrightarrow\left[{}\begin{matrix}\left(2x+1\right)^2=\left(\frac{2}{3}\right)^2\\\left(2x+1\right)^2=\left(-\frac{2}{3}\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+1=\frac{2}{3}\\2x+1=-\frac{2}{3}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=-\frac{1}{3}\\2x=-\frac{5}{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\frac{1}{6}\\x=-\frac{5}{6}\end{matrix}\right.\)
Vậy \(x\in\left\{-\frac{1}{6};-\frac{5}{6}\right\}\)


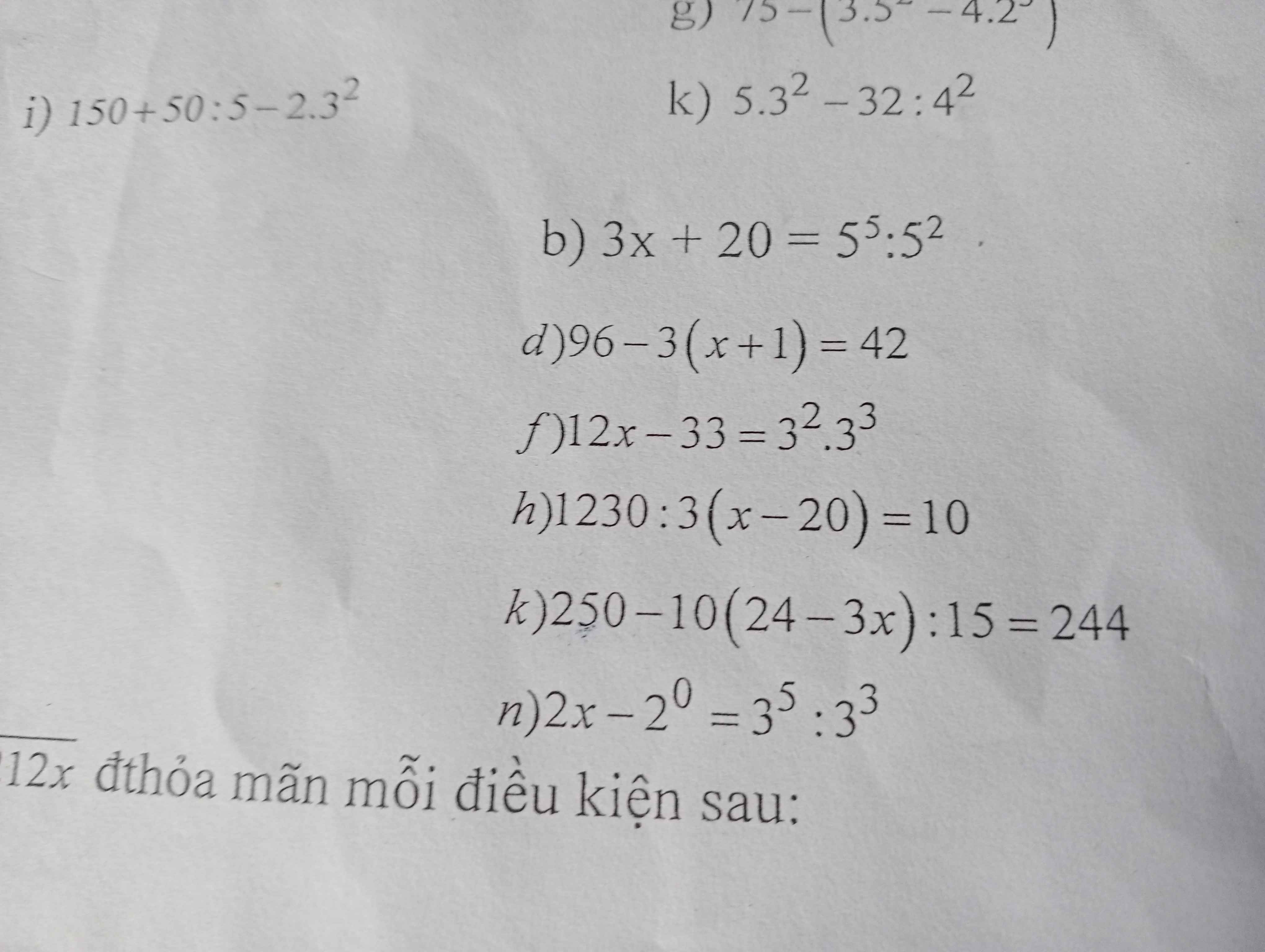
a+b=-m; b+m=-a; a+m=-b
A=(a+b)/b*(m+b)/m*(m+a)/a=-1