 giair giúp mình
giair giúp mình
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1) Ta có: \(x-2\sqrt{x}=0\)
\(\Leftrightarrow\sqrt{x}\left(\sqrt{x}-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\end{matrix}\right.\)
2) Ta có: \(6+\sqrt{x}-x=0\)
\(\Leftrightarrow x-\sqrt{x}-6=0\)
\(\Leftrightarrow\left(\sqrt{x}-3\right)\left(\sqrt{x}+2\right)=0\)
\(\Leftrightarrow\sqrt{x}-3=0\)
\(\Leftrightarrow x=9\)
3) Ta có: \(x+3\sqrt{x}-4=0\)
\(\Leftrightarrow\left(\sqrt{x}+4\right)\left(\sqrt{x}-1\right)=0\)
\(\Leftrightarrow\sqrt{x}-1=0\)
\(\Leftrightarrow x=1\)

d: Xét ΔABK và ΔCKB có
AB=CK
KB chung
AK=CB
Do đó: ΔABK=ΔCKB

= 232x 98 -123 x 98
= 98 x ( 232 - 123)
=98 x 109
=10682 Hình như sai đề bài à
= 232 x 98 - 123 x 98
= 98 x ( 132 - 123 )
= 98 x 109
= 10682
~~~~hok tốt~~~~

khó quá ha lờ e tờ ét lờ ét lét huyền ... từ bn muốn đánh vần ý

\(x^2\left(x^2-4\right)=3\left(x^2-4\right)\)
\(\Rightarrow x^2\left(x^2-4\right)-3\left(x^2-4\right)=0\)
\(\Rightarrow\left(x^2-4\right)\left(x^2-3\right)=0\)
\(\Rightarrow\left[\begin{array}{nghiempt}x^2-4=0\\x^2-3=0\end{array}\right.\)
\(\Rightarrow\left[\begin{array}{nghiempt}\left[\begin{array}{nghiempt}x=2\\x=-2\end{array}\right.\\\left[\begin{array}{nghiempt}x=\sqrt{3}\\x=-\sqrt{3}\end{array}\right.\end{array}\right.\)
Vậy x=2; x= - 2 ; x=\(\sqrt{3}\) ; x=\(-\sqrt{3}\)
Có : \(x^2\left(x^2-4\right)=3\left(x^2-4\right)\)
\(\Leftrightarrow x^2\left(x^2-4\right)-3\left(x^2-4\right)=0\)
\(\Leftrightarrow\left(x^2-4\right)\left(x^2-3\right)=0\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}x^2-4=0\\x^2-3=0\end{array}\right.\) \(\Leftrightarrow\left[\begin{array}{nghiempt}x^2=4\\x^2=3\end{array}\right.\) \(\Leftrightarrow\left[\begin{array}{nghiempt}x=2;x=-2\\x=\sqrt{3};x=-\sqrt{3}\end{array}\right.\)
Vậy \(x=-2;x=2;x=-\sqrt{3};x=\sqrt{3}\)


ĐKXĐ: ...
\(\sqrt{x^2-x-30}-3\sqrt{x+5}-2\sqrt{x-6}=-6\)
\(\Leftrightarrow\sqrt{\left(x+5\right)\left(x-6\right)}-3\sqrt{x+5}-2\sqrt{x-6}=-6\)(*)
đặt \(\sqrt{x+5}=a\ge0;\sqrt{x-6}=b\ge0\)
\(\text{pt(*)}\Leftrightarrow ab-3a-2b=-6\\ \Leftrightarrow\Leftrightarrow ab-3a-2b+6=0\\ \Leftrightarrow a\left(b-3\right)-2\left(b-3\right)=0\\ \Leftrightarrow\left(a-2\right)\left(b-3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}a=2\\b=3\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}\sqrt{x+5}=2\\\sqrt{x-6}=3\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x+5=4\\x-6=9\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=-1\left(ktm\right)\\x=15\left(tm\right)\end{matrix}\right.\)

Nhìn nó có dạng \(\sqrt{\left(\sqrt{a}+\sqrt{b}+\sqrt{c}\right)^2}=\sqrt{a+b+c+2\left(\sqrt{ab}+\sqrt{bc}+\sqrt{ca}\right)}\)
Thấy \(2\left(\sqrt{6}+\sqrt{12}+\sqrt{18}\right)=2\left(\sqrt{2.3}+\sqrt{2.6}+\sqrt{3.6}\right)\)
nên:
\(\sqrt{11+2\left(\sqrt{6}+\sqrt{12}+\sqrt{18}\right)}=\sqrt{\sqrt{2}^2+\sqrt{6}^2+\sqrt{3}^2+2\left(\sqrt{2.3}+\sqrt{2.6}+\sqrt{3.6}\right)}\)
\(=\sqrt{\left(\sqrt{2}+\sqrt{3}+\sqrt{6}\right)^2}=\sqrt{2}+\sqrt{3}+\sqrt{6}\)

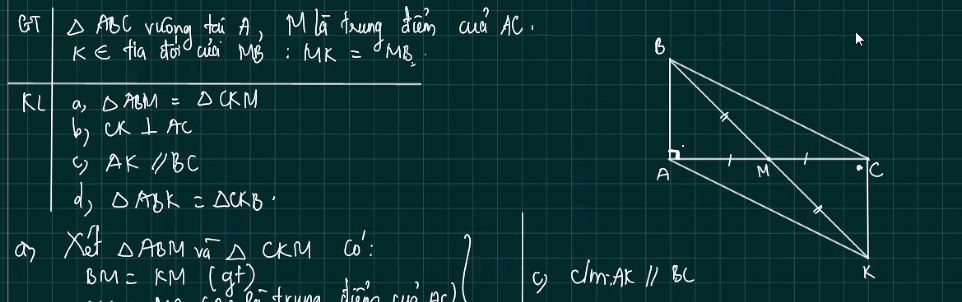 giúp mình câu d với
giúp mình câu d với 