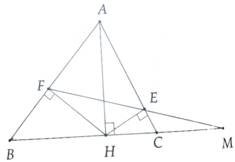
Bài 8: Cho tam giác ABC nhọn, AB < AC các đường cao AD, BE, CF đồng quy tại trực tâm H.
1. Chứng minh HE HB = HF HC.
2. Chứng minh AF.AB=AE.AC=AH.AD và góc AFE = góc ACB = góc AHE
3. AH cắt EF tại I.Chứng minh IA.IH=IE.IF
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét (O) có
ΔBFC nội tiếp
BC là đường kính
Do đó: ΔBFC vuông tại F
Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔBEC vuông tại E
Xét ΔABC có
BE,CF là đường cao
BE cắt CF tại H
Do đó: AH vuông góc với BC tại D
b: Xét ΔAEH vuông tại E và ΔADC vuông tại D có
góc EAH chung
Do đó: ΔAEH đồnbg dạng với ΔADC
Suy ra: AE/AD=AH/AC
hay \(AE\cdot AC=AH\cdot AD\)

a, Ta có: ∆AEF ~ ∆MCE (c.g.c)
=> A F E ^ = A C B ^
b, Ta có: ∆MFB ~ ∆MCE (g.g)
=> ME.MF = MB.MC

a: góc BFC=góc BEC=90 độ
=>BFEC nội tiêp
=>góc AFE=góc ACB
mà góc FAE chung
nên ΔAFE đồng dạng với ΔACB
b: Xét ΔDAB vuông tại D và ΔDCH vuông tại D có
góc DAB=góc DCH
=>ΔDAB đồng dạng vơi ΔDCH
=>DA/DC=DB/DH
=>DA*DH=DB*DC
c: Xét ΔHDC vuông tại D và ΔHFA vuông tại F có
góc DHC=góc FHA
=>ΔHDC đồng dạng vơi ΔHFA
=>HD/HF=HC/HA
=>HF*HC=HD*HA
Xet ΔHFB vuông tại F và ΔHEC vuông tại E có
góc FHB=góc EHC
=>ΔHFB đồng dạng với ΔHEC
=>HF/HE=HB/HC
=>HF*HC=HB*HE=HD*HA

3:
Xét ΔCEH vuông tại E và ΔCFA vuông tại F có
\(\widehat{FCA}\) chung
Do đó: ΔCEH đồng dạng với ΔCFA
=>CE/CF=CH/CA
=>\(CE\cdot CA=CH\cdot CF\)
Xét ΔCDH vuông tại D và ΔCFB vuông tại F có
\(\widehat{FCB}\) chung
Do đó: ΔCDH đồng dạng với ΔCFB
=>CD/CF=CH/CB
=>CD*CB=CH*CF
=>CD*CB=CH*CF=CE*CA
Xét ΔBDH vuông tại D và ΔBEC vuông tại E có
\(\widehat{EBC}\) chung
Do đó: ΔBDH đồng dạng với ΔBEC
=>BD/BE=BH/BC
=>\(BD\cdot BC=BH\cdot BE\)
Xét ΔBDA vuông tại D và ΔBFC vuông tại F có
góc DBA chung
Do đó: ΔBDA đồng dạng với ΔBFC
=>BD/BF=BA/BC
=>BD*BC=BF*BA
=>BD*BC=BF*BA=BH*BE
\(AH\cdot AD+BH\cdot BE=AF\cdot AB+BF\cdot BA=BA^2\)
\(AH\cdot AD+CH\cdot CF=AE\cdot AC+CE\cdot CA=AC^2\)
\(BH\cdot BE+CH\cdot CF=BD\cdot BC+CD\cdot CB=BC^2\)
Do đó: \(2\left(AH\cdot AD+BH\cdot BE+CH\cdot CF\right)=BA^2+AC^2+BC^2\)
=>\(AH\cdot AD+BH\cdot BE+CH\cdot CF=\dfrac{AB^2+AC^2+BC^2}{2}\)

a: Xét ΔHFB vuông tại F và ΔHEC vuông tại E có
góc FHB=góc EHC
=>ΔHFB đồng dạng với ΔHEC
=>HF/HE=HB/HC
=>HF*HC=HE*HB
b: góc BFC=góc BEC=90 độ
=>BFEC nội tiếp
=>góc BFE+góc BCE=180 độ
mà góc AFE+góc BFE=180 độ
nên góc AFE=góc ACB
c: Xét ΔKFB và ΔKCE có
góc KFB=góc KCE(=góc AFE)
góc K chung
=>ΔKFB đồng dạng với ΔKCE
=>KF/KC=KB/KE
=>KF*KE=KB*KC
1: Xét ΔHFB vuông tại F và ΔHEC vuông tại E có
góc FHB=góc EHC
=>ΔHFB đồng dạng với ΔHEC
=>HF/HE=HB/HC
=>HF*HC=HB*HE
2: Xét ΔAFH vuông tại F và ΔADB vuông tại D có
góc FAH chung
=>ΔAFH đồng dạng với ΔADB
=>AF/AD=AH/AB
=>AF*AB=AD*AH
Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
góc EAB chung
=>ΔAEB đồng dạng với ΔAFC
=>AE/AF=AB/AC
=>AE*AC=AB*AF=AH*AD