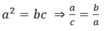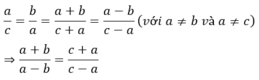Chứng minh rằng nếu a2=bc với a ≠ b và a ≠ c thì a+ b/ a-b = c+a/c-a. Giúp mik nhà mik sẽ tick cho
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: \(\dfrac{a}{b}=\dfrac{c}{d}\Leftrightarrow\dfrac{b}{a}=\dfrac{d}{c}\)
\(\Leftrightarrow1+\dfrac{b}{a}=1+\dfrac{d}{c}\)
\(\Leftrightarrow\dfrac{a+b}{a}=\dfrac{c+d}{c}\)
\(\dfrac{a}{b}=\dfrac{c}{d}\Leftrightarrow\dfrac{a}{c}=\dfrac{b}{d}\)
Áp dụng t/c dtsbn:
\(\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{a+b}{c+d}\Leftrightarrow\dfrac{a+b}{a}=\dfrac{c+d}{c}\)

\(\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\dfrac{a}{c}=\dfrac{b}{d}\)
\(\left\{{}\begin{matrix}\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{a-b}{c-d}\\\dfrac{a}{c}=\dfrac{b}{d}\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}\left(\dfrac{a}{c}\right)^2=\dfrac{\left(a-b\right)^2}{\left(c-d\right)^2}\\\left(\dfrac{a}{c}\right)^2=\dfrac{ab}{cd}\end{matrix}\right.\)
\(\Rightarrow\dfrac{ab}{cd}=\dfrac{\left(a-b\right)^2}{\left(c-d\right)^2}\)

Em kiểm tra lại đề bài nhé! Tham khảo link:
Câu hỏi của Phan Thúy Vy - Toán lớp 7 - Học toán với OnlineMath

Bạn ghi sai đề rồi. Qui tắc cộng phân số là "qui đồng mẫu số trước"
Mình nghĩ đề là \(\frac{a}{b}=\frac{c}{d}=\frac{a+b}{c+d}\). Mình làm theo đề này :
Đặt \(\frac{a}{b}=\frac{c}{d}=k\) => a = bk ; c = dk
Ta có : \(\frac{a+b}{c+d}=\frac{bk+b}{dk+d}=\frac{b\left(k+1\right)}{d\left(k+1\right)}=\frac{b}{d}\); mà \(\frac{a}{b}=\frac{c}{d}\Leftrightarrow\frac{a}{c}=\frac{b}{d}\) (t/c tỉ lệ thức)
Do đó \(\frac{a}{b}=\frac{c}{d}=\frac{a+b}{c+d}\)
ko phải vậy đâu. cô mình cho đề này vs lại mình cũng có quyển đó sorry nha! nhưng mình vẫn sẽ tick cho bn