Giúp e làm cái 26 vẽ hình giải chi tiết, 27 nua ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DT
0
DP
Cho hình thang ABCD(AB//CD). Tìm độ dài x trong các hình vẽ bên dưới
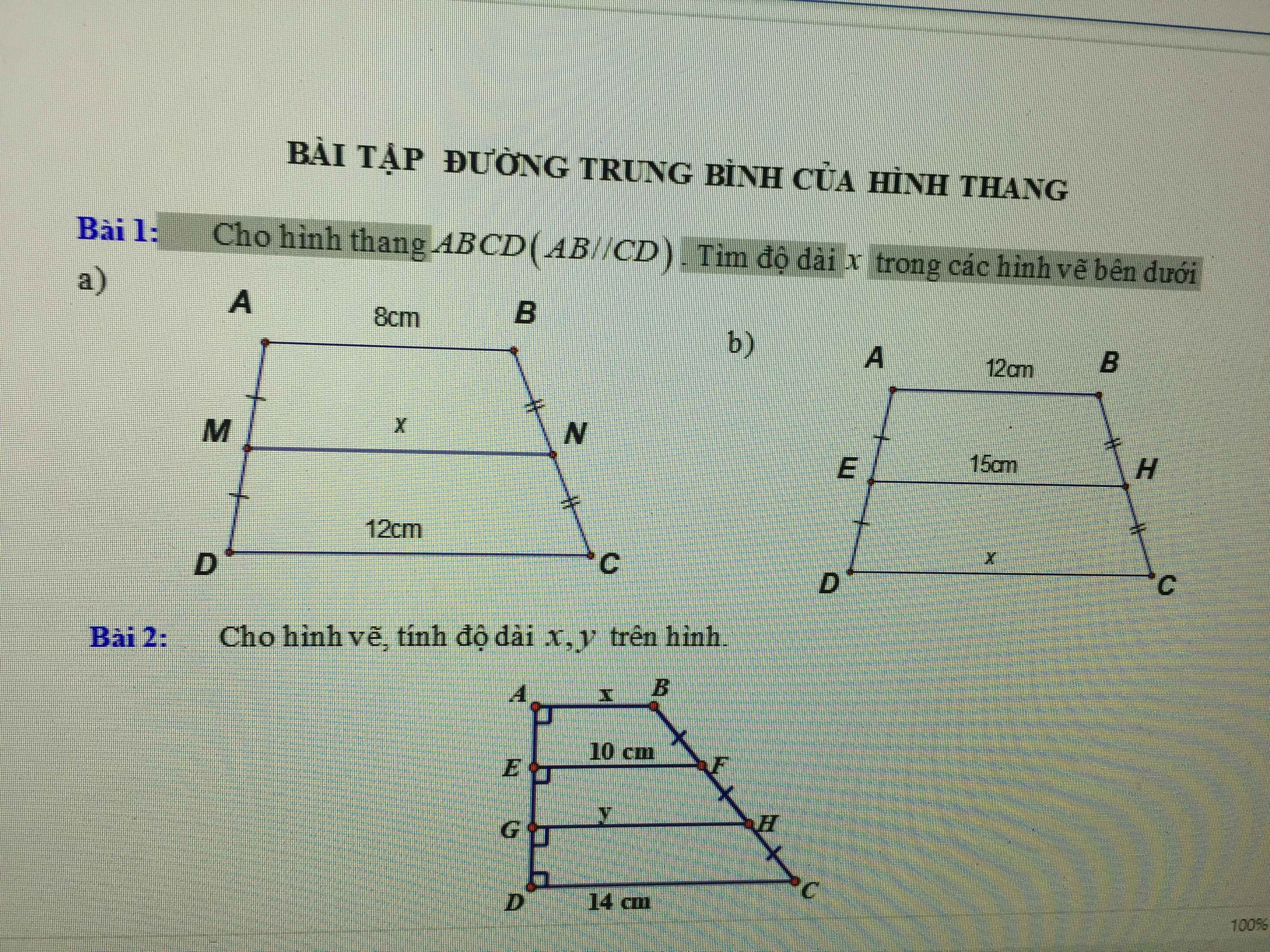
Giải chi tiết giúp mình nha
0
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 5 2021
1. \(y'=6x^2+6x\Rightarrow y'\left(1\right)=12\)
Đáp án B
2. \(y'=\dfrac{7}{\left(x+3\right)^2}\Rightarrow y'\left(1\right)=\dfrac{7}{16}\) (A)
3. \(y'=8x^3+9x^2-3\Rightarrow y'\left(3\right)=294\)
Tất cả các đáp án đều sai
4. Tiếp tục là 1 câu đề bài sai
Hàm số không xác định tại \(x=1\Rightarrow\) không liên tục tại \(x=1\Rightarrow\) không tồn tại đạo hàm tại \(x=1\)
5.
\(f'\left(x\right)=7x^6+20x^4+6x\)
\(\Rightarrow f'\left(2\right)=780\)
6.
\(y'=\dfrac{3}{\left(x+1\right)^2}\)
\(\Rightarrow y'\left(2\right)=\dfrac{1}{3}\) ; \(y\left(2\right)=1\)
Phương trình tiếp tuyến:
\(y=\dfrac{1}{3}\left(x-2\right)+1\Leftrightarrow y=\dfrac{1}{3}x+\dfrac{1}{3}\)
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 2 2022
\(\int\limits^2_1\dfrac{2x+1}{x^2+x}dx=\int\limits^2_1\dfrac{d\left(x^2+x\right)}{x^2+x}=ln\left(x^2+x\right)|^2_1=ln6-ln2=ln3\)
\(\Rightarrow\left\{{}\begin{matrix}a=0\\b=3\end{matrix}\right.\) \(\Rightarrow a^2+b^2=9\)
C1
1
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 1 2022
3.
\(\left|x-2\right|=2-x\Leftrightarrow\left|2-x\right|=2-x\)
\(\Leftrightarrow2-x\ge0\Rightarrow x\le2\) (quy tắc trị tuyệt đối: \(\left|A\right|=A\Leftrightarrow A\ge0\))
6. Đề bài sai (có lẽ do in nhầm)
Tập xác định của pt này là R
8.
Đặt \(\sqrt{x^2+3x+3}=t>0\Rightarrow x^2+3x+1=t^2-2\)
\(\Rightarrow t^2+t-2=0\Rightarrow\left[{}\begin{matrix}t=1\\t=-2\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow x^2+3x+3=1\Rightarrow\left[{}\begin{matrix}x=-1\\x=-2\end{matrix}\right.\)
9.
\(\Leftrightarrow\left|\left(x+1\right)\left(x+4\right)\right|=x+4\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+4\ge0\\\left[{}\begin{matrix}x+4=0\\\left|x+1\right|=1\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ge-5\\\left[{}\begin{matrix}x=-4\\x=0\\x=-2\end{matrix}\right.\end{matrix}\right.\) (3 nghiệm đều thỏa mãn)
C1
2
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 1 2022
29.
Do \(M\in\Delta\) nên tọa độ có dạng: \(M\left(m;2m+1\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AM}=\left(m-4;2m+4\right)\\\overrightarrow{BM}=\left(m-5;2m-4\right)\\\overrightarrow{CM}=\left(m-1;2m+2\right)\end{matrix}\right.\)
\(\Rightarrow AM^2+BM^2+CM^2\)
\(=\left(m-4\right)^2+\left(2m+4\right)^2+\left(m-5\right)^2+\left(2m-4\right)^2+\left(m-1\right)^2+\left(2m+2\right)^2\)
\(=15m^2-12m+78\)
\(=15\left(m-\dfrac{2}{5}\right)^2+\dfrac{378}{5}\ge\dfrac{378}{5}\)
Dấu "=" xảy ra khi \(m=\dfrac{2}{5}\Rightarrow M\left(\dfrac{2}{5};\dfrac{9}{5}\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 1 2022
30.
Đặt \(f\left(x\right)=x^2-6x-7\)
Đồ thị hàm \(y=\left|f\left(x\right)\right|=\left|x^2-6x-7\right|\) được tạo ra bằng cách lấy đối xứng phần bên dưới trục Ox của đồ thị \(f\left(x\right)\) lên như hình vẽ:
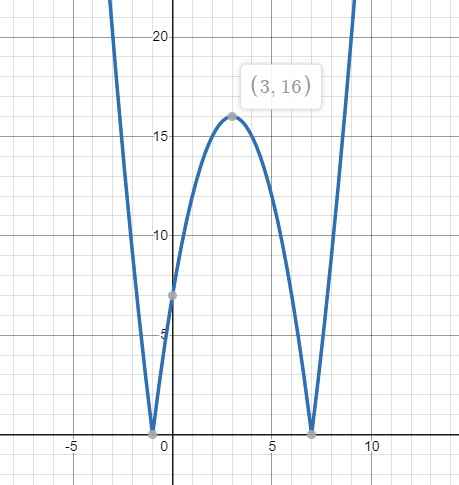
Từ đồ thị ta thấy pt có 4 nghiệm pb khi và chỉ khi: \(0< m< 16\)
\(\Rightarrow\) Có 15 giá trị nguyên của m
C1
1
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 4 2022
35.
\(y'=5cos^4\left(2-3x\right).\left[cos\left(2-3x\right)\right]'\)
\(=5cos^4x.\left(-sin\left(2-3x\right)\right).\left(2-3x\right)'\)
\(=15cos^4\left(2-3x\right).sin\left(2-3x\right)\)
\(\Rightarrow\left\{{}\begin{matrix}m=15\\n=4\end{matrix}\right.\) \(\Rightarrow m+n=19\)
36.
\(U_2=2-\dfrac{1}{2}=\dfrac{3}{2}\) ; \(u_3=2-\dfrac{1}{\dfrac{3}{2}}=\dfrac{4}{3}\) ; \(u_5=2-\dfrac{1}{\dfrac{4}{3}}=\dfrac{5}{4}\)
\(\Rightarrow\) Quy nạp được \(u_n=\dfrac{n+1}{n}\)
\(\Rightarrow\lim\left(u_n\right)=\lim\dfrac{n+1}{n}=1\)
37.
\(\lim\limits_{x\rightarrow3}\dfrac{\sqrt{x^2+7}-4}{2x-6}=\lim\limits_{x\rightarrow3}\dfrac{x^2-9}{2\left(x-3\right)\left(\sqrt{x^2+7}+4\right)}\)
\(=\lim\limits_{x\rightarrow3}\dfrac{\left(x-3\right)\left(x+3\right)}{2\left(x-3\right)\left(\sqrt{x^2+7}+4\right)}\)
\(=\lim\limits_{x\rightarrow3}\dfrac{x+3}{2\left(\sqrt{x^2+7}+4\right)}=\dfrac{6}{2\left(\sqrt{9+7}+4\right)}=\dfrac{3}{8}\)
Hàm liên tục trên R khi:
\(\dfrac{3}{8}=1-2m\Rightarrow m=\dfrac{5}{16}\in\left(0;1\right)\)
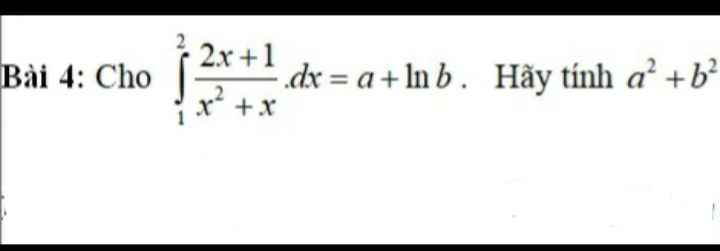
27:
=lim[n^3(-5-1/n+1/n^3)]=-vô cực
26B