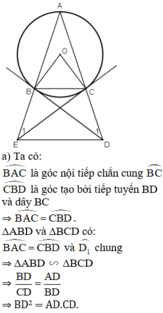
Cho ΔABC cân tại A (với AB > BC) nội tiếp đường tròn (O). Tiếp tuyến tại B và C của đường tròn lần lượt cắt tia AC và tia AB tại D và E. Hãy
a) Chứng minh:
b) Chứng minh tứ giác BCDE nội tiếp.
c) Chứng minh: BC // DE
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b) ΔABC cân tại A
⇒ AB = AC
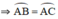
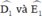 là các góc có đỉnh ở bên ngoài đường tròn nên ta có:
là các góc có đỉnh ở bên ngoài đường tròn nên ta có:
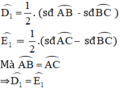
⇒ D và E cùng nhìn BC dưới 1 góc bằng nhau
⇒ BCDE là tứ giác nội tiếp.
c. Tứ giác BCDE nội tiếp

⇒ BC // DE (hai góc đồng vị bằng nhau).

b) ΔABC cân tại A
⇒ AB = AC
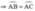
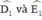 là các góc có đỉnh ở bên ngoài đường tròn nên ta có:
là các góc có đỉnh ở bên ngoài đường tròn nên ta có:
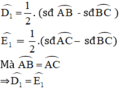
⇒ D và E cùng nhìn BC dưới 1 góc bằng nhau
⇒ BCDE là tứ giác nội tiếp.
c. Tứ giác BCDE nội tiếp

⇒ BC // DE (hai góc đồng vị bằng nhau).

a) Chứng minh tam giác MAB đồng dạng tam giác MFC
b) Chứng minh góc \(\widehat{BKF}=\widehat{FAD}\)
c) E là trực tâm của \(\Delta MBC\)suy ra MH vuông góc BC ... suy ra tứ giác MDBH là hình thang
d) \(\Delta BHE\)đồng dạng \(\Delta BAC\)... suy ra BE.BA=BC.BH
\(\Delta CHE\)đồng dạng \(\Delta CFB\)... suy ra CE.CF=CB.CH
BE.BA+CE.CF=BC.BH+CB.CH=BC(BH+CH)=BC.BC=BC^2

B1, a, Xét tứ giác AEHF có: góc AFH = 90o ( góc nội tiếp chắn nửa đường tròn)
góc AEH = 90o (góc nội tiếp chắn nửa đường tròn )
Góc CAB = 90o ( tam giác ABC vuông tại A)
=> tứ giác AEHF là hcn(đpcm)
b, do AEHF là hcn => cũng là tứ giác nội tiếp => góc AEF = góc AHF ( hia góc nội tiếp cùng chắn cung AF)
mà góc AHF = góc ACB ( cùng phụ với góc FHC)
=> góc AEF = góc ACB => theo góc ngoài tứ giác thì tứ giác BEFC là tứ giác nội tiếp (đpcm)
c,gọi M là giao điểm của AI và EF
ta có:góc AEF = góc ACB (c.m.t) (1)
do tam giác ABC vuông tại A và có I là trung điểm của cạng huyền CB => CBI=IB=IA
hay tam giác IAB cân tại I => góc MAE = góc ABC (2)
mà góc ACB + góc ABC + góc BAC = 180o (tổng 3 góc trong một tam giác)
=> ACB + góc ABC = 90o (3)
từ (1) (2) và (3) => góc AEF + góc MAE = 90o
=> góc AME = 90o (theo tổng 3 góc trong một tam giác)
hay AI uông góc với EF (đpcm)

Ta có: \(\widehat{CDF}=\widehat{CAD}\) (cùng chắn AD)
\(\widehat{CAD}=\widehat{BAD}\) (AD là phân giác)
\(\widehat{BAD}=\widehat{BCD}\) (cùng chắn BD)
\(\Rightarrow\widehat{CDF}=\widehat{BCD}\)
\(\Rightarrow BC||EF\) (hai góc so le trong bằng nhau)
\(\Rightarrow\dfrac{AB}{AE}=\dfrac{AC}{AF}\Rightarrow AB.AF=AC.AE\)
Cũng từ BC song song EF \(\Rightarrow\widehat{ACB}=\widehat{AFD}\) (đồng vị)
Mà \(\widehat{ACB}=\widehat{ADB}\) (cùng chắn AB)
\(\Rightarrow\widehat{AFD}=\widehat{ADB}\)
Xét 2 tam giác AFD và ADB có:
\(\left\{{}\begin{matrix}\widehat{FAD}=\widehat{DAB}\left(\text{AD là phân giác}\right)\\\widehat{AFD}=\widehat{ADB}\left(cmt\right)\end{matrix}\right.\) \(\Rightarrow\Delta AFD\sim\Delta ADB\left(g.g\right)\)
\(\Rightarrow\dfrac{AD}{AB}=\dfrac{AF}{AD}\Rightarrow AB.AF=AD^2\)
\(\Rightarrow AB.AF=AC.AE=AD^2\)

a: góc OAD+góc OMD=180 độ
=>OADM nội tiếp
b: ΔOBC cân tại O
mà ON là đường cao
nên ONlà trung trực của BC
=>sđ cung NB=sd cung NC
=>góc BAN=góc CAN
=>AN là phân giác của góc BAC
góc DAI=1/2*sđ cung AN
góc DIA=1/2(sđ cung AB+sđ cung NC)
=1/2(sđ cung AB+sđ cung NB)
=1/2*sđ cung AN
=>góc DAI=góc DIA
=>ΔDAI cân tại D
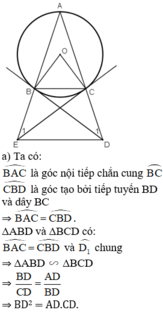
a) Xét (O) có
\(\widehat{BAC}\) là góc nội tiếp chắn cung BC
\(\widehat{DBC}\) là góc tạo bởi dây cung BC và tiếp tuyến BD
Do đó: \(\widehat{BAC}=\widehat{DBC}\)(Hệ quả góc tạo bởi tiếp tuyến và dây cung)