Cho tam giác ABC vuông góc tai A và đường cao AH . gọi E và D theo thứ tự là hình chiếu của H trên AC và M là Trung điểm của cạnh BC .Chứng minh :
a) DE = AH
b) AM vuông góc DE
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
8 tháng 10 2019
Vì ADHE là hình chữ nhật nên OD = OH
Suy ra, tam giác ODH cân tại O ⇒ ∠ ODH = ∠ OHD
Mà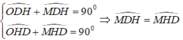 
Xét tam giác MBD có:
∠ (MDB) = ∠ (MBD) (vì cùng phụ với hai góc bằng nhau ∠ (MDH) = ∠ (MHD))
Suy ra, tam giác MBD cân tại M, do đó MD = MB (2)
Từ (1) và (2) suy ra, MB = MH
Vậy M là trung điểm của BH
Tương tự, ta cũng có N là trung điểm của CH.
28 tháng 1 2022
a, Xét tứ giác ADHE có :
^A = ^ADH = ^HEA = 900
Vậy tứ giác ADHE là hcn
Vậy AH = DE ( 2 đường chéo bằng nhau )
b, Xét tam giác AEH và tam giác AHC có :
^AEH = ^AHC = 900
^A _ chung
Vậy tam giác AEH ~ tam giác AHC ( g.g )
=> AH/AC = AE/AH => AH^2 = AE.AC (1)
tương tự với tam giác ADH ~ tam giác AHB (g.g)
=> AD/AH = AH/AB => AH^2=AD.AB (2)
Từ (1) ; (2) suy ra AE.AC = AD.AB
c, Xét tam giác ABH và tam giác CAH
^AHB = ^CHA = 900
^ABH = ^CAH ( cùng phụ ^BAH )
Vậy tam giác ABH ~ tam giác CAH (g.g)
=> AH/CH = BH/AH => AH^2 = BH.CH
=> CH = AH^2/BH = 144/9 = 16
=> BC = BH + CH = 25 cm
Diện tích tam giác ABC là : SABC = 1/2 . AH . BC
= 1/2 . 12 . 25 = 150 cm2
21 tháng 12 2023
Sửa đề: D,E lần lượt là hình chiếu của H trên AB,AC
a: Xét tứ giác ADHE có
\(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)
=>ADHE là hình chữ nhật
b: Ta có: ADHE là hình chữ nhật
=>\(\widehat{AED}=\widehat{AHD}\)
mà \(\widehat{AHD}=\widehat{B}\left(=90^0-\widehat{HAB}\right)\)
nên \(\widehat{AED}=\widehat{B}\)
Ta có: ΔABC vuông tại A
mà AM là đường trung tuyến
nên MA=MB=MC
Ta có: MA=MC
=>ΔMAC cân tại M
=>\(\widehat{MAC}=\widehat{MCA}\)
Ta có: \(\widehat{MAC}+\widehat{AED}\)
\(=\widehat{MCA}+\widehat{B}\)
\(=90^0\)
=>AM\(\perp\)DE
c: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=6^2+8^2=100\)
=>\(BC=\sqrt{100}=10\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot10=6\cdot8=48\)
=>\(AH=\dfrac{48}{10}=4,8\left(cm\right)\)
Ta có: ADHE là hình chữ nhật
=>DE=AH
mà AH=4,8cm
nên DE=4,8cm
26 tháng 8 2022
Xét tứ giác ADHE có góc ADH=góc AEH=góc EAD=90 độ
nên ADHE là hình chữ nhật
=>góc AED=góc AHD=góc ABC
Ta có: ΔABC vuông tại A
mà AM là đường trung tuyến
nên MA=MC
=>ΔMAC cân tại M
=>góc MAC=góc MCA
=>góc MAC+góc AED=90 độ
=>AM vuông góc với DE
18 tháng 12 2023
a:
Sửa đề: Là hình chiếu của H trên AB,AC
Xét tứ giác ADHE có
\(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)
=>ADHE là hình chữ nhật
b: Ta có: ΔABC vuông tại A
mà AM là đường trung tuyến
nên MA=MB=MC
Ta có: MA=MC
=>\(\widehat{MAC}=\widehat{MCA}\)
Ta có: ADHE là hình chữ nhật
=>\(\widehat{AED}=\widehat{AHD}\)
mà \(\widehat{AHD}=\widehat{ABC}\left(=90^0-\widehat{HAD}\right)\)
nên \(\widehat{AED}=\widehat{ABC}\)
\(\widehat{AED}+\widehat{MAC}\)
\(=\widehat{ABC}+\widehat{ACB}=90^0\)
=>AM\(\perp\)DE
c: Ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=6^2+8^2=100\)
=>\(BC=\sqrt{100}=10\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot10=6\cdot8=48\)
=>AH=48/10=4,8(cm)
Ta có: ADHE là hình chữ nhật
=>AH=DE
mà AH=4,8cm
nên DE=4,8cm
18 tháng 11 2023
Xét tứ giác ADHE có
\(\widehat{ADH}=\widehat{AEH}=\widehat{EAD}=90^0\)
=>ADHE là hình chữ nhật
=>\(\widehat{AED}=\widehat{AHD}\)
mà \(\widehat{AHD}=\widehat{ABC}\left(=90^0-\widehat{HAB}\right)\)
nên \(\widehat{AED}=\widehat{ABC}\)
ΔABC vuông tại A
mà AM là đường trung tuyến
nên MA=MC=MB
MA=MC
=>ΔMAC cân tại M
=>\(\widehat{MAC}=\widehat{MCA}=\widehat{ACB}\)
\(\widehat{MAC}+\widehat{AED}=\widehat{ACB}+\widehat{ABC}=90^0\)
=>AM vuông góc DE
a, Xét tứ giác DHEA có :
góc Â=90
góc D=90
góc E=90
Mà trong tứ giác có 3 góc vuông là hình chữ nhật
Vậy tứ giác DHEA là HCN
Mà ta có trong hình chữ nhật có 2 đường chéo cắt nhau tại trung điểm mỗi đường thì bằng nhau
Suy ra : DE=AH
b,Cần c/m tam giác AHM
Thì suy ra : AH=AM
Mà AH vuông góc với DE ( 2đg chéo của hình chữ nhật DHEA )
Nên : AM sẽ vuông góc với DE (đpcm)
k cho mình nha ! Thanks !