một bãi cỏ hình vuông được bao bởi hàng rào có diện tích là 100 mét vuông . Ở một góc của bãi cỏ đó có một gốc cây và một con bò đang đứng . Một sợi dây thừng 5m buộc vào gốc cây. Hỏi diện tích phần cỏ tối đa con bò ăn được là bao nhiêu, biết diện tích gốc cây không đáng kể
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

con dê vì dê ăn cỏ ko với được và hổ ko ăn cỏ nên nó sẽ ăn con dê .

Đáp án A
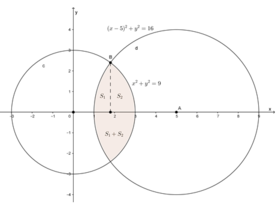
Ta giải bằng phương pháp gắn hệ tọa độ Oxy, với gốc tọa độ O chính là chỗ cây cộc buộc con bò có sợi dây dài 3m, trục Ox là đường nối 2 cây cộc buộc dây của 2 con bò, ta được như hình vẽ.
Khi đó con bò có sợi dây 3m có thể ăn cỏ trong hình tròn giới hạn bởi đường tròn có bán kính 3m và có phương trình đường tròn tâm O là
![]()
là đường phía trên trục hoành. Ta cũng có phần cỏ của con bò có sợi dây 4m bị hạn chế trong đường tròn có phương trình tâm A, bán kính 4 là
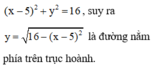
Giao điểm của 2 đường tròn này là nghiệm của hệ 2 pt đường tròn đó
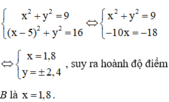
Ta chỉ cần tính phần diện tích phía trên trục hoành, phần dưới trục hoành có độ lớn cũng bằng như vậy. Từ B ta vẽ đường nét đứt vuông góc với Ox để chia đôi phần cần tính diện tích phía trên trục hoành, ta có


đc chứ sao ko , dây thừng thắt dưới gốc cây chứ đâu có thắt nó vào gốc cây mà ko đi đc , vẫn đi ăn cỏ đc thôi
có chứ . dây thừng buộc ở gốc cây chứ có buộc vào chân nó đâu.
t i c k cho tớ nhé.


Kiến thức áp dụng
+ Diện tích hình tròn bán kính R là: S = πR2.

Theo các buộc thứ nhất thì diện tích cỏ dành cho mỗi con dê là bằng nhau.
Mỗi diện tích là 1/4 hình tròn bán kính 20m.
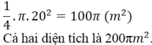 (1)
(1)
Theo cách thuộc thứ hai, thì diện tích cỏ dành cho con dê buộc A là:

So sánh (1) và (2) ta thấy với cách buộc thứ 2 thì diện tích cỏ mà hai con dê có thể ăn được sẽ lớn hơn

Gọi x là chiều rộng bãi cỏ thì chiều dài bãi cỏ sẽ là 1000 - 2x
Khi đó diện tích bãi cỏ là:
S = x( 1000 - 2x ) = 1000x - 2 x 2 .
Ta có S'(x) = 1000 - 4x = 0 nên x = 250
Vậy max S = S (250) = 125000 m 2
Đáp án D



