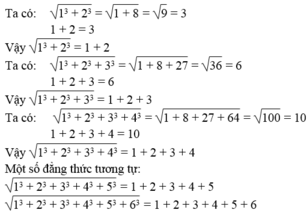Chứng minh rằng : 13+23+33+43+.....+n3= ( 1 + 2 + 3 + 4 + ...... + n )2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
29 tháng 9 2019
Đặt vế trái bằng A n
Dễ thấy với n = 1 hệ thức đúng.
Giả sử đã có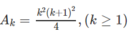 
Ta có:
KV
22 tháng 10 2023
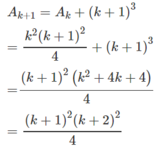
a) P = 1 + 3 + 3² + ... + 3¹⁰¹
= (1 + 3 + 3²) + (3³ + 3⁴ + 3⁵) + ... + (3⁹⁹ + 3¹⁰⁰ + 3¹⁰¹)
= 13 + 3³.(1 + 3 + 3²) + ... + 3⁹⁹.(1 + 3 + 3²)
= 13 + 3³.13 + ... + 3⁹⁹.13
= 13.(1 + 3³ + ... + 3⁹⁹) ⋮ 13
Vậy P ⋮ 13
b) B = 1 + 2² + 2⁴ + ... + 2²⁰²⁰
= (1 + 2² + 2⁴) + (2⁶ + 2⁸ + 2¹⁰) + ... + (2²⁰¹⁶ + 2²⁰¹⁸ + 2²⁰²⁰)
= 21 + 2⁶.(1 + 2² + 2⁴) + ... + 2²⁰¹⁶.(1 + 2² + 2⁴)
= 21 + 2⁶.21 + ... + 2²⁰¹⁶.21
= 21.(1 + 2⁶ + ... + 2²⁰¹⁶) ⋮ 21
Vậy B ⋮ 21
c) A = 2 + 2² + 2³ + ... + 2²⁰
= (2 + 2² + 2³ + 2⁴) + (2⁵ + 2⁶ + 2⁷ + 2⁸) + ... + (2¹⁷ + 2¹⁸ + 2¹⁹ + 2²⁰)
= 30 + 2⁴.(2 + 2² + 2³ + 2⁴) + ... + 2¹⁶.(2 + 2² + 2³ + 2⁴)
= 30 + 2⁴.30 + ... + 2¹⁶.30
= 30.(1 + 2⁴ + ... + 2¹⁶)
= 5.6.(1 + 2⁴ + ... + 2¹⁶) ⋮ 5
Vậy A ⋮ 5
d) A = 1 + 4 + 4² + ... + 4⁹⁸
= (1 + 4 + 4²) + (4³ + 4⁴ + 4⁵) + ... + (4⁹⁷ + 4⁹⁸ + 4⁹⁹)
= 21 + 4³.(1 + 4 + 4²) + ... + 4⁹⁷.(1 + 4 + 4²)
= 21 + 4³.21 + ... + 4⁹⁷.21
= 21.(1 + 4³ + ... + 4⁹⁷) ⋮ 21
Vậy A ⋮ 21
e) A = 11⁹ + 11⁸ + 11⁷ + ... + 11 + 1
= (11⁹ + 11⁸ + 11⁷ + 11⁶ + 11⁵) + (11⁴ + 11³ + 11² + 11 + 1)
= 11⁵.(11⁴ + 11³ + 11² + 11 + 1) + 16105
= 11⁵.16105 + 16105
= 16105.(11⁵ + 1)
= 5.3221.(11⁵ + 1) ⋮ 5
Vậy A ⋮ 5
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
16 tháng 8 2023
Bài 1:
13 + 23 = 1 + 8 = 9 = 32 (là một số chính phương)
13 + 23 + 33 = 1 + 8 + 27 = 36 = 62 (là một số chính phương)
13 + 23 + 33 + 43 = 1 + 8 + 27 + 64 = 100 = 102 (là số cp)
13 + 23 + 33 + 43 + 53 = 1 + 8 + 27 + 64 + 125 = 225 = (15)2 là số cp
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
16 tháng 8 2023
Bài 2:
1262 + 1 = \(\overline{..6}\) + 1 = \(\overline{...7}\) (không phải số chính phương)
100! + 8 = \(\overline{...0}\) + 8 = \(\overline{...8}\) (không phải là số chính phương)
1012 - 3 \(\overline{..01}\) - 3 = \(\overline{...8}\) (không phải là số chính phương)
107 + 7 = \(\overline{..0}\) + 7 = \(\overline{..7}\) (không phải là số chính phương)
11 + 112 + 113 = \(\overline{..1}\)+ \(\overline{..1}\)+ \(\overline{..1}\) = \(\overline{...3}\) (không phải số chính phương)
VK
3
18 tháng 10 2015
Ta có: B = (1 + 100) + (2 + 99) + ...+ (50 + 51) = 101. 50
Để chứng minh A chia hết cho B ta chứng minh A chia hết cho 50 và 101
Ta có: A = (13 + 1003) + (23 + 993) + ... +(503 + 513)
= (1 + 100)(12 + 100 + 1002) + (2 + 99)(22 + 2. 99 + 992) + ... + (50 + 51)(502 + 50. 51 + 512) =
101(12 + 100 + 1002 + 22 + 2. 99 + 992 + ... + 502 + 50. 51 + 512) chia hết cho 101 (1)
Lại có: A = (13 + 993) + (23 + 983) + ... + (503 + 1003)
Mỗi số hạng trong ngoặc đều chia hết cho 50 nên A chia hết cho 50 (2)
Từ (1) và (2) suy ra A chia hết cho 101 và 50 nên A chi hết cho B
18 tháng 10 2015
Ta có: B = (1 + 100) + (2 + 99) + ...+ (50 + 51) = 101. 50
Để chứng minh A chia hết cho B ta chứng minh A chia hết cho 50 và 101
Ta có: A = (13 + 1003) + (23 + 993) + ... +(503 + 513)
= (1 + 100)(12 + 100 + 1002) + (2 + 99)(22 + 2. 99 + 992) + ... + (50 + 51)(502 + 50. 51 + 512) =
101(12 + 100 + 1002 + 22 + 2. 99 + 992 + ... + 502 + 50. 51 + 512) chia hết cho 101 (1)
Lại có: A = (13 + 993) + (23 + 983) + ... + (503 + 1003)
Mỗi số hạng trong ngoặc đều chia hết cho 50 nên A chia hết cho 50 (2)
Từ (1) và (2) suy ra A chia hết cho 101 và 50 nên A chi hết cho B
VK
0
KV
23 tháng 12 2023
A = 8⁸ + 2²⁰
= (2³)⁸ + 2²⁰
= 2²⁴ + 2²⁰
= 2²⁰.(2⁴ + 1)
= 2²⁰.17 ⋮ 17
Vậy A ⋮ 17
10 tháng 10 2021
\(B=2+2^2+2^3+...+2^{60}\)
\(=2\left(1+2+2^2\right)+...+2^{58}\left(1+2+2^2\right)\)
\(=7\cdot\left(2+...+2^{58}\right)⋮7\)
5 tháng 5 2018
\(\dfrac{5}{2x1}+\dfrac{4}{1x11}+\dfrac{3}{11x2}+\dfrac{1}{2x15}+\dfrac{13}{15x4}+\dfrac{15}{4x13}\)
=7x(\(\dfrac{5}{2x7}+\dfrac{4}{7x11}+\dfrac{3}{11x14}+\dfrac{1}{14x15}+\dfrac{13}{15x28}+\dfrac{15}{28x43}\))
=7x\(\dfrac{1}{2}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{11}+\dfrac{1}{11}-\dfrac{1}{14}+\dfrac{1}{14}-\dfrac{1}{15}+\dfrac{1}{15}-\dfrac{1}{28}+\dfrac{1}{28}-\dfrac{1}{43}\)=7x(\(\dfrac{1}{2}-\dfrac{1}{43}\))
=7x\(\dfrac{41}{86}\)
=\(\dfrac{287}{86}\)
5 tháng 5 2018
5/2x1+4/1x11+3/11x2+1/2x15+13/15x4+15/4x43=7x(5/2x7+4/7x11+3/11x14+1/14x15+13/15x28+15/28x43)=7x(1/2-1/7+1/7-1/11+1/11-1/14+1/14+1/15+1/15-1/28+1/28-1/43)=7x(1/2-1/43)=7x41/86=287/86