Đặt vật AB trước một TKPK có tiêu cự f=32cm A nằm trên trục chính .biết ảnh A'B' Cao Bằng 1/4 vật AB xác định vị trí vật và ảnh?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ảnh thật, ngược chiều và lớn hơn vật.
Vị trí đặt ảnh:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{20}=\dfrac{1}{30}+\dfrac{1}{d'}\Rightarrow d'=60cm\)
Chiều cao ảnh:
\(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow\dfrac{4,5}{h'}=\dfrac{30}{60}\Rightarrow h'=9cm\)

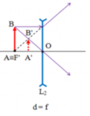
Vật AB đặt trước thấu kính phân kỳ có tiêu cự f, có A nằm trên trục chính và cách thấu kính một khoảng OA cho ảnh A′B′ cao bằng nửa vật AB khi OA=OF′=f
Đáp án: B

Vị trí ảnh:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{20}=\dfrac{1}{30}+\dfrac{1}{d'}\Rightarrow d'=60cm\)
Chiều cao ảnh:
\(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow\dfrac{20}{h'}=\dfrac{30}{60}\Rightarrow h'=40cm\)

a. Dựng ảnh A'B'

b) d > f , ảnh lớn hơn và ngược chiều với vật
c)
Tóm tắt:
OF = 12cm
OA = 18cm
AB = 6cm
A'B' = ?
Giải:
Δ ABF ~ OIF
\(\Rightarrow\dfrac{AB}{OI}=\dfrac{AF}{OF}\Leftrightarrow\dfrac{AB}{A'B'}=\dfrac{OA-OF}{OF}\Leftrightarrow\dfrac{6}{A'B'}=\dfrac{18-12}{12}\)
=> A'B' = 12cm

(đề bài), ...và cách thấu kính 12cm à (hình anh tự vẽ )
\(=>d< f\left(12cm< 20cm\right)\)=>ảnh tạo bới vật AB qua thấu kính hội tụ là ảnh ảo , lớn hơn vật và cùng chiều vật
\(=>\dfrac{1}{f}=\dfrac{1}{d}-\dfrac{1}{d'}=>\dfrac{1}{20}=\dfrac{1}{12}-\dfrac{1}{d'}=>d'=30cm\)
=>ảnh cách tk 30cm
\(=>\dfrac{h}{h'}=\dfrac{d}{d'}=>\dfrac{2}{h'}=\dfrac{12}{30}=>h'=5cm\)
=>ảnh A'B' cao 5cm
\(=>\)khoảng cách giữa ảnh với vật d+d'=42cm

a) Ta có: \(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\)
\(\Rightarrow d'=\dfrac{18.12}{18-12}=36\left(cm\right)\)
\(k=\dfrac{-d}{d}=\dfrac{-36}{18}=-2\)
Ảnh thật cách thấu kính 18cm, ngược chiều với vật, hệ số phóng đại k=-2
b) Để thu được ảnh cao bằng 3 lần vật thì d < f ; d' < 0
Ta có: k = 3 (ảnh cùng chiều với vật)
\(\Rightarrow\dfrac{-d'}{d}=3\) \(\Rightarrow d'=-3d\)
Ta có: \(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\)
\(\Rightarrow d=16\left(cm\right)\)