Cho hình chữ nhật ABCD. Kẻ BK vuông góc với AC. Gọi M , N lần lượt là trung điểm AK và CĐ . Biết B(1;2), N(-3;0) . Viết phương trình đường tròn ngoại tiếp tam giác BM
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 12 2023
a: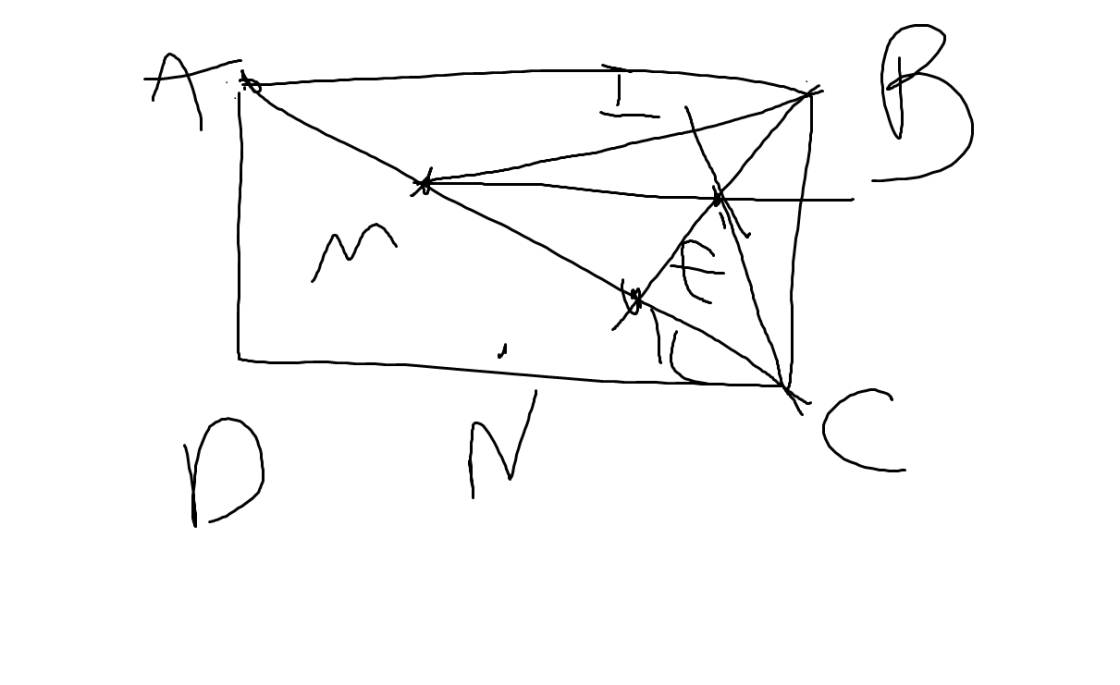 
b: Xét ΔBMC có
BK,CI là các đường cao
BK cắt CI tại E
Do đó: E là trực tâm của ΔBMC
=>ME\(\perp\)BC
mà AB\(\perp\)BC
nên ME//AB
Xét ΔKAB có
M là trung điểm của KA
ME//AB
Do đó: E là trung điểm của BK
=>BE=EK
c: Xét ΔKAB có
M,E lần lượt là trung điểm của KA,KB
=>ME là đường trung bình của ΔKAB
=>\(ME=\dfrac{AB}{2}\)
mà AB=CD(ABCD là hình chữ nhật)
và \(NC=\dfrac{CD}{2}\)(N là trung điểm của CD)
nên ME=NC
Ta có: ME//AB
CD//AB
Do đó: ME//CD
Xét tứ giác MNCE có
ME//CN
ME=CN
Do đó: MNCE là hình bình hành
d: ta có: MNCE là hình bình hành
=>MN//CE
mà CE\(\perp\)MB
nên MN\(\perp\)MB
12 tháng 11 2023
Xét ΔBNC có
CI,BK là đường cao
CI cắt BK tại E
Do đó: E là trực tâm của ΔBNC
=>NE\(\perp\)BC
mà AB\(\perp\) BC
nên NE//AB
Xét ΔKAB có
N là trung điểm của KA
NE//AB
Do đó; E là trung điểm của BK
=>EB=EK
CM
13 tháng 1 2018
Chọn B.
Xét đáp án B
Đặt 
và BA = a; BC = b và BK = c.
Do M là trung điểm của AK nên 
,
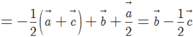
Do đó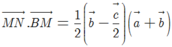 
Vì 
và 
nên 
Suy ra MN và BM vuông góc với nhau
Do đó góc BMN bằng 900.