Lm giupmk câu c thôi a
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(B=\dfrac{\left(3x+1\right)^2-\left(3x-1\right)^2}{\left(3x-1\right)\left(3x+1\right)}\cdot\dfrac{6x-2}{3}\)
\(=\dfrac{9x^2+6x+1-9x^2+6x-1}{3x+1}\cdot\dfrac{2}{3}\)
\(=\dfrac{12x}{3\left(3x+1\right)}=\dfrac{4x}{3x+1}\)
b: B>-2
=>B+2>0
=>\(\dfrac{4x+6x+2}{3x+1}>0\)
=>\(\dfrac{10x+2}{3x+1}>0\)
=>x>-1/3 hoặc x<-1/5
c: B=3
=>4x=3(3x+1)
=>9x+3=4x
=>5x=-3
=>x=-3/5

a, \(AC=\sqrt{BC^2-AB^2}=16\left(cm\right)\)
\(AH=\dfrac{AB\cdot AC}{BC}=9,6\left(cm\right)\\ \sin ABC=\dfrac{AC}{BC}=\dfrac{4}{5}\approx\sin53^0\Rightarrow\widehat{ABC}\approx53^0\)
b, Áp dụng HTL: \(AN\cdot AC=AH^2\)
Áp dụng PTG: \(AH^2=AC^2-HC^2\)
Suy ra đpcm
c, Vì \(\widehat{AMH}=\widehat{ANH}=\widehat{MAN}=90^0\) nên AMHN là hcn
Do đó AH=MN
Áp dụng HTL: \(\left\{{}\begin{matrix}AN\cdot NC=HN^2\\AM\cdot MB=HM^2\end{matrix}\right.\)
Áp dụng PTG: \(HN^2+HM^2=MN^2=AH^2\)
Suy ra đpcm

Bài 1
3 helpers (thêm s là dc r)
4 megacities
Bài 2
4 D
5 B
8 D
10 D
III
2 puts
5 Will you go
IV
1 Because this movie is very exciting, we want to see it
2 Should your brother work harder, he will win the first prize
3 Because of the bad weather, we stayed at home
4 Unless you get up early tomorrow, you will be late for the meeting
5 Because of his good acting( ko biết acting hay action nx ), the film was a great success


a)\(đkx\ge1,x\ne-1\)
\(\sqrt{\dfrac{x-1}{x+1}}=2\)
\(\Leftrightarrow\dfrac{x-1}{x+1}=4\)
\(\Leftrightarrow x-1=4x-4\)
\(\Leftrightarrow x=1\)(nhận)
Vậy S=\(\left\{1\right\}\)
c)đk\(25x^2-10x+1=\) \(\left(5x-1\right)^2\ge0\Leftrightarrow x\ge\dfrac{1}{5}\)
\(\sqrt{25x^2-10x+1}+2x=1\)
\(\Leftrightarrow\sqrt{\left(5x-1\right)^2}+2x=1\)
\(\Leftrightarrow5x-1+2x=1\)
\(\Leftrightarrow x=\dfrac{2}{7}\)(nhận)
Vậy S=\(\left\{\dfrac{2}{7}\right\}\)
c: Ta có: \(\sqrt{25x^2-10x+1}+2x=1\)
\(\Leftrightarrow\left|5x-1\right|=1-2x\)
\(\Leftrightarrow\left[{}\begin{matrix}5x-1=1-2x\left(x\ge\dfrac{1}{5}\right)\\5x-1=2x-1\left(x< \dfrac{1}{5}\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{2}{7}\left(nhận\right)\\x=0\left(nhận\right)\end{matrix}\right.\)

c. \(\left(x+2\right)^4-6\left(x+2\right)^2+5=0\)
\(\Leftrightarrow\left(x+2\right)^4-\left(x+2\right)^2-5\left(x+2\right)^2+5=0\)
\(\Leftrightarrow\left(x+2\right)^2\left[\left(x+2\right)^2-1\right]-5\left[\left(x+2\right)^2-1\right]=0\)
\(\Leftrightarrow\left[\left(x+2\right)^2-1\right]\left[\left(x+2\right)^2-5\right]=0\)
\(\Leftrightarrow\left(x+3\right)\left(x+1\right)\left(x+2+\sqrt{5}\right)\left(x+2-\sqrt{5}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+3=0\\x+1=0\\x+2+\sqrt{5}=0\\x+2-\sqrt{5}=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=-1\\x=-\sqrt{5}-2\\x=\sqrt{5}-2\end{matrix}\right.\)
Vậy: Phương trình có tập nghiệm \(S=\left\{-3;-1;-\sqrt{5}-2;\sqrt{5}-2\right\}\)


a: Xét ΔBHD vuông tại H và ΔENC vuông tại N có
BD=EC
\(\widehat{BDH}=\widehat{ECN}\)
Do đó: ΔBHD=ΔENC

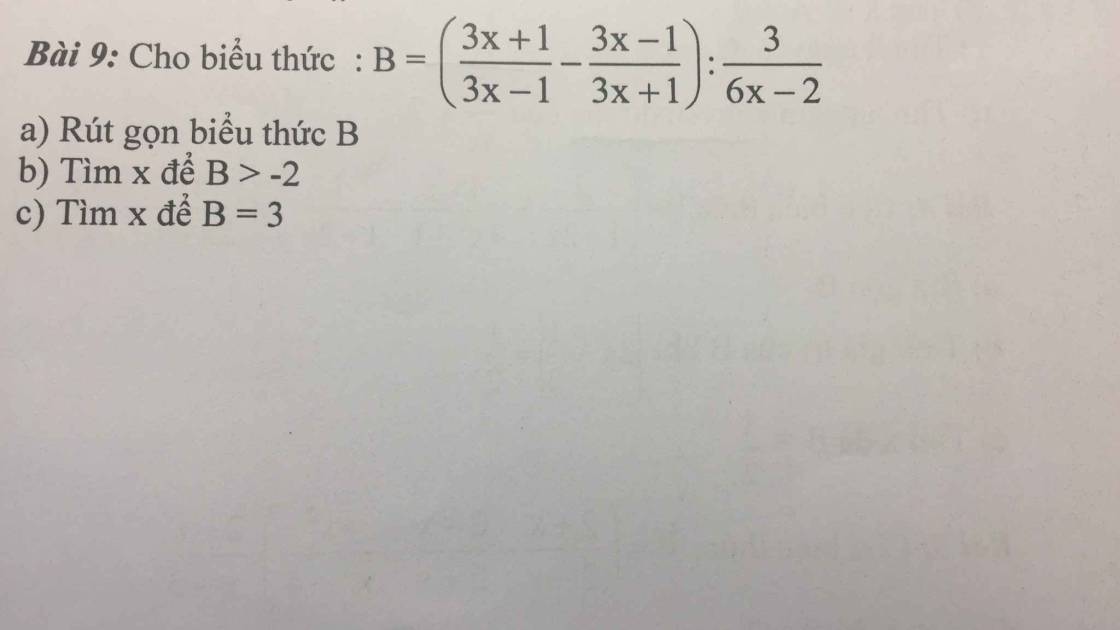 lm câu b và c thôi nhé! cảm ơn ạ!
lm câu b và c thôi nhé! cảm ơn ạ!








