cho hình chóp SABCD có đáy là hình vuông cạnh a các mặt đều là những tam giác đều cạnh a. tính góc giữa
a) (SAB) và (ABCD)
b) (SCD) và (SBC)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 5 2021
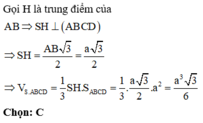
Gọi H là trung điểm AB \(\Rightarrow SH\perp AB\Rightarrow SH\perp\left(ABCD\right)\Rightarrow SH\perp BC\)
Mà \(BC\perp AB\Rightarrow BC\perp\left(SAB\right)\)
Gọi K là trung điểm CD \(\Rightarrow HK||BC\Rightarrow HK\perp AB\Rightarrow HK\perp\left(SAB\right)\)
Trong tam giác SHK, kẻ \(HI\perp SK\Rightarrow HI\perp\left(SCD\right)\)
\(\Rightarrow HI=d\left(H;\left(SCD\right)\right)\)
Mà \(AH||CD\Rightarrow AH||\left(SCD\right)\Rightarrow d\left(A;\left(SCD\right)\right)=d\left(H;\left(SCD\right)\right)=HI\)
\(SH=\dfrac{AB\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{2}\) ; \(HK=BC=a\)
\(\dfrac{1}{HI^2}=\dfrac{1}{SH^2}+\dfrac{1}{HK^2}=\dfrac{7}{3a^2}\Rightarrow HI=\dfrac{a\sqrt{21}}{7}\)
b. Theo cmt ta có \(BC\perp\left(SAB\right)\Rightarrow d\left(C;\left(SAB\right)\right)=BC=a\)
c. \(BC||AD\Rightarrow d\left(C;\left(SAD\right)\right)=d\left(B;\left(SAD\right)\right)\)
Mà BH cắt (SAD) tại A, đồng thời \(BA=2HA\Rightarrow d\left(B;\left(SAD\right)\right)=2d\left(H;\left(SAD\right)\right)\)
Từ H kẻ \(HM\perp SA\Rightarrow HM\perp\left(SAD\right)\Rightarrow HM=d\left(H;\left(SAD\right)\right)\)
\(\dfrac{1}{HM^2}=\dfrac{1}{SH^2}+\dfrac{1}{AH^2}=\dfrac{16}{3a^2}\Rightarrow HM=\dfrac{a\sqrt{3}}{4}\)
\(\Rightarrow d\left(C;\left(SAD\right)\right)=2HM=\dfrac{a\sqrt{3}}{2}\)
CM
1 tháng 4 2018
Đáp án là A
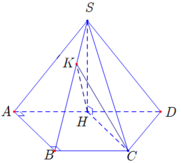
Gọi H là trung điểm của A B . Gọi K là hình chiếu vuông góc của H lên S B .
Khi đó, C K H ^ là góc giữa hai mp
Ta có: S H = 2 a 3 2 = a 3 ; S B = 2 a ; H B = a ⇒ H K = a 3 2 ; C K = a 7 2 .
Vậy cos C K H ^ = 3 7
CM
6 tháng 12 2017
Phương pháp:
Công thức tính thể tích khối chóp có diện tích đáy S và chiều cao h là: V = 1 3 S h
Cách giải:
HP
17 tháng 6 2021
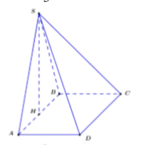
Kẻ SH vuông góc AB tại H.
a, Ta có: \(h=SH=AH.tan\alpha=2a\)
\(\Rightarrow V=\dfrac{1}{3}.B.h=\dfrac{1}{3}.\left(2a\right)^2.2a=\dfrac{8a^3}{3}\)
b, \(SB=BC.tan\alpha=2\sqrt{5}a\Rightarrow SH=\sqrt{SB^2-BH^2}=\sqrt{19}a\)
\(\Rightarrow V=\dfrac{1}{3}.B.h=\dfrac{1}{3}.\left(2a\right)^2.\sqrt{19}a=\dfrac{4\sqrt{19}a^3}{3}\)
c, Kẻ HI vuông góc với CD.
Ta có: \(SH=HI.tan\alpha=6a\)
\(\Rightarrow V=\dfrac{1}{3}.B.h=\dfrac{1}{3}.\left(2a\right)^2.6a=8a^3\)
