Cho 3 số a,b,c với 0<a<b<c. Biết rằng tổng 2 số nhỏ nhất được lập từ 3 số a,b,c ở trên bằng 488
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LT
Cho các số a, b, c thỏa mãn a^3+ b^3+ c^3= 3abc với a, b, c khác 0. Chứng minh a+ b+c = 0 hoặc a=b=c
1
15 tháng 1 2021
a3 + b3 + c3 = 3abc
⇒ a3 + b3 + c3 - 3abc = 0
⇒ ( a3 + b3 ) + c3 - 3abc = 0
⇒ ( a + b )3 - 3ab( a + b ) + c3 - 3abc = 0
⇒ [ ( a + b )3 + c3 ] - [ 3ab( a + b ) + 3abc ] = 0
⇒ ( a + b + c )[ ( a + b )2 - ( a + b ).c + c2 ] - 3ab( a + b + c ) = 0
⇒ ( a + b + c )( a2 + b2 + c2 - ab - bc - ac ) = 0
⇒ \(\orbr{\begin{cases}a+b+c=0\\a^2+b^2+c^2-ab-bc-ac=0\end{cases}}\)
+) a2 + b2 + c2 - ab - bc - ac = 0
⇒ 2( a2 + b2 + c2 - ab - bc - ac ) = 2.0
⇒ 2a2 + 2b2 + 2c2 - 2ab - 2bc - 2ac = 0
⇒ ( a2 - 2ab + b2 ) + ( b2 - 2bc + c2 ) + ( a2 - 2ac + c2 ) = 0
⇒ ( a - b )2 + ( b - c )2 + ( a - c )2 = 0
VT ≥ 0 ∀ a,b,c . Dấu "=" xảy ra khi a = b = c
⇒ a + b + c = 0 hoặc a = b = c ( đpcm )
CM
27 tháng 4 2017
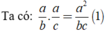
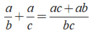
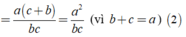
Từ (1), (2) ta có:
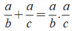với b + c = a (a, b, c ∈ Z, b ≠ 0, c ≠ 0)
Nếu a = 8, b = -3 thì c = a - b = 8 - (-3) = 11
21 tháng 11 2018
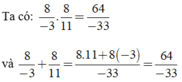
Theo bài ra: \(\frac{a+b}{6}=\frac{b+c}{4}=\frac{c+a}{3}\)
Đặt \(\frac{a+b}{6}=\frac{b+c}{4}=\frac{c+a}{3}=t\left(t\ne0\right)\Rightarrow a+b=6t,b+c=4t,c+a=3t\)
\(\Rightarrow\left(a+b\right)+\left(b+c\right)+\left(c+a\right)=6t+4t+3t\)
\(\Rightarrow2\left(a+b+c\right)=13t\Rightarrow a+b+c=6,5t\)
Ta có: \(a=\left(a+b+c\right)-\left(b+c\right)=6,5t-4t=2,5t\)
\(b=\left(a+b\right)-a=6t-2,5t=3,5t\)
\(c=\left(a+c\right)-a=3t-2,5t=0,5t\)
Ta có: \(b-a=3,5t-2,5t=t\)
\(a-c=2,5t-0,5t=2t\)
\(b-c=3,5t-0,5t=3t\)
Vậy \(\left(b-a\right):\left(a-c\right):\left(b-c\right)=t:\left(2t\right):\left(3t\right)=1:2:3\)
hay b - a , a - c và b - c tỉ lệ thuận với 1,2,3
Vì 0 < a < b < c nên 2 số nhỏ nhất được lập từ 3 số a, b, c là abc và acb.
Theo bài ra ta có:
abc
+ acb
488
Xét phép cộng cột hàng chục và đơn vị ta thấy c + b không nhớ.
=> a + a = 4 => 2a = 4 => a = 4: 2 = 2
Từ 2 < b < c và b + c = 8
=> b = 3, c = 5
Vậy a = 2, b = 3, c = 5