Một phân số có hiệu giữa mẫu số và tử số là 12. Nếu cùng thêm vào tử số và mẫu số của phân số đó với 4 đơn vị thì ta được một phân số mới có giá trị bằng \(\dfrac{5}{9}\). Tìm phân số ban đầu.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi phân số cũ là : a/15
Thì phân số mới là : (a-10)/25
Ta có phương trình :
(a-10)/25 = 8/5 . a/15 <=> (3a-30)/75 = 8a/75
=> 3a - 30 = 8a <=> -5a = 30 <=> x = -6
Vậy phân số đó là : -6/15 = -2/5

Gọi phân số cũ là : \(\frac{a}{15}\)
Thì phân số mới là : \(\frac{a-10}{25}\)
Ta có phương trình :
\(\frac{a-10}{25}=\frac{8}{5}.\frac{a}{15}\Leftrightarrow\frac{3a-30}{75}=\frac{8a}{75}\)
\(\Rightarrow3a-30=8a\Leftrightarrow-5a=30\Leftrightarrow x=-6\)
Vậy phân số đó là : \(\frac{-6}{15}=\frac{-2}{5}\)

1) Nếu chuyển từ mẫu số lên tử số \(12\)đơn vị thì tổng của tử số và mẫu số không đổi.
Khi đó tử số mới là:
\(210\div2=105\)
Tử số ban đầu là:
\(105-12=93\)
Mẫu số ban đầu là:
\(210-93=117\)
Phân số cần tìm là: \(\frac{93}{117}\).
2) Nếu thêm \(9\)đơn vị vào tử số thì tổng tử số mới và mẫu số là:
\(175+9=184\)
Tử số mới hay mẫu số là:
\(184\div2=92\)
Tử số là:
\(92-9=83\)
Phân số cần tìm là: \(\frac{83}{92}\).

gọi tử số của phân số cần tìm là a
mẫu số của phân số cần tìm là a+5
nêu thêm tử 17 đơn zị , mẫu 2 đơn zị thì ta có
\(\frac{a+17}{a+7}\)
theo đề bài t có phương trình
\(\frac{a+17}{a+7}=\frac{a+5}{a}\)\(\Leftrightarrow\)\(a\left(a+17\right)=\left(a+5\right)\left(a+7\right)\Leftrightarrow a^2+17a=a^2+7a+5a+35\)
=>\(5a=35=>a=7\)
phâ số cần tìm là \(\frac{7}{12}\)

Gọi tử số của phân số ban đầu là a, theo bài ra ta có:
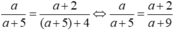
(Điều kiện: a ≠ - 5;a ≠ - 9 )
a(a + 9) = (a + 2)(a + 5)
⇔ a 2 + 9 a = a 2 + 7 a + 10
⇔ 2a = 10 ⇔ a = 5 (Thỏa mãn)
Vậy phân số cần tìm là: 5/10

Nếu cả tử và mẫu cùng thêm 4 đơn vị vào tử số và mẫu số thì hiện vẫn ko thay đổi.
\(\dfrac{5}{9}\) = \(\dfrac{15}{27}\)
\(\dfrac{15-4}{27-4}=\dfrac{11}{23}\)
11/23 nhé
HT