Cho năm chữ số 1;2;3;4;5. Có thể lập được bao nhiêu số có bốn chữ số khác nhau, biết rằng các số đó đều chia hết cho 5.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
a) Gọi số thỏa mãn đề có dạng $\overline{abcd}$ với $a,b,c,d$ khác nhau.
Nếu $a=1$:
$b=2$ thì $(c,d)=(3,4), (4,3), (3,5),(5,3),(4,5)(5,4)$, tức là có 6 giá trị thỏa mãn
$b=3$ tương tự cũng có 6 giá trị thỏa mãn
$b=4$ tương tự cũng có 6 giá trị thỏa mãn
$b=5$ tương tự cũng có 6 giá trị thỏa mãn
Tóm lại với $a=5$ có $6+6+6+6=24$ số thỏa mãn
Tương tự với $a=2,3,4,5$ cũng vậy
Suy ra có thể viết được: $5\times 24=120$ số.
b) Vẫn gọi số cần tìm là $\overline{abcd}$. Số chẵn sẽ có tận cùng là $2$ hoặc $4$
Nếu $d=2$ thì lập luận tương tự phần $b$ ta viết được $24$ số $\overline{abcd}$
Nếu $d=4$ ta cũng viết được $24$ số
Do đó, viết được: $24+24=48$ số chẵn.

2. Dãy số có 4 chữ số chia hết cho 3 là: 1002;1005;1008;.....;9999
Số các số có 4 chữ số chia hết cho 3 là: (9999 - 1002) : 3 + 1 = 3000 số
Giải (1)
Có thể lập được các số có 5, 4, 3, 2 chữ số.
Xét về 5 chữ số: a b c d e:
a có 4 lựa chọn (lc)
b có 4 lc
c có 3 lc
d có 2 lc
e có 1 lc
Vậy có tất cả các số khác nhau có 5 chữ số: 4 × 4 × 3 × 2 × 1 = 96 (số)
Xét về 4 chữ số: a b c d
a có 4 lc
b có 4 lc
c có 3 lc
d có 2 lc
Vậy... : 4 × 4 × 3 × 2 = 96 (số)
Tự làm ...
Xét về 3 chữ số có 48 (số) Xét về 2 chữ số có 16 (số)
Vậy ... 96 + 96 + 48 + 16 = 256 (số)
Đ/s:..
Giải (2)
Cách 1:
Số đầu tiên có 4 chữ số chia hết cho 3 là: 1002
Số cuối cùng có 4 chữ số chia hết cho 3 là: 9999
Vì khoảng cách giữa 2 số là 3 đơn vị và ta có công thức:
(Số cuối - số đầu) ÷ khoảng cách + 1
=> (9999 - 1002) ÷ 3 + 1 = 3000 (số)
Đ/s:

Vì mỗi số đều chia hết cho 5. Suy ra: Tất cả các số này đều có chữ số tận cùng là: 5
Vì là số có 5 chữ số khác nhau nên ta có:
1 cách chọn chữ số hàng đơn vị (chữ số 5)
5 cách chọn chữ số hàng chục nghìn (loại chữ số 5)
4 cách chọn chữ số hàng nghìn (loại chữ số 5 và chữ số hàng chục nghìn)
3 cách chọn chữ số hàng trăm (loại chữ số 5, chữ số hàng chục nghìn và chữ số hàng nghìn)
2 cách chọn chữ số hàng chục (loại chữ số 5, chữ số hàng chục nghìn, chữ số hàng nghìn và chữ số hàng trăm)
Theo quy tắc nhân, ta có: Số số có 5 chữ số khác nhau mà mỗi số đều chia hết cho 5, lập được từ các chữ số trên là: 1 x 5 x 4 x 3 x 2 = 120 (số)
Suy ra:
Mỗi chữ số 1, 2, 3, 7, 9 xuất hiện số lần là: 120 : 5 = 24 (lần)
Riêng chữ số 5 xuất hiện 120 lần
Suy ra: Tổng là:
(1 + 2 + 3 + 7 + 9) x 24 x 10000 + (1 + 2 + 3 + 7 + 9) x 24 x 1000 + (1 + 2 + 3 + 7 + 9) x 24 x 100 + (1 + 2 + 3 + 7 + 9) x 24 x 10 + 5 x 120
= 22 x 24 x (10000 + 1000 + 100 + 10) + 5 x 120
= 22 x 24 x 11110 + 5 x 120
= 5866080 + 600
= 5866680

số số hạng là:
5x4x3x2x1=120
có số chữ số là : 120x5 =600(chữ số )
chữ số 5 xuất hiện ở hàng đon vị 120 lần
5 chữ số còn lại xuất hiện số lần là: 600-120=480(lần)
vai trò của các chữ số là như nhau nên mỗi chữ số xuất hiện số lần là : 480 : 5=96(lần)
các chữ số xuất hiện ở hàng chục nghìn ,hàng nghìn ,hàng trăm ,hàng chục số lần là: 96:4=24 (lần)
vậy tổng các chữ số có chưc số khác nhau chia hết cho 5 viết từ các chữ số đã cho là:
(1+2+3+4+6)x 24 x10 000=3 840 000
(1+2+3+4+6)x24 x1000=384 000
(1+2+3+4+6)x24x100=38 400
(1+2+4+6)x24x10+120x5=4440
vậy tổng bằng 4266840

Đáp án D
Từ các số đã cho, số lớn nhất có năm chữ số khác nhau được tạo thành là 53210
Từ các số đã cho, số bé nhất có bốn chữ số khác nhau được tạo thành là 10235
Tổng của hai số vừa tìm được là: 53210 + 10235 = 63445
Đáp số: 63445.

Đáp án C
Từ các số đã cho, số lớn nhất có bốn chữ số khác nhau được tạo thành là: 53210
Từ các số đã cho, số bé nhất có bốn chữ số khác nhau được tạo thành là: 10235
Hiệu của hai số vừa tìm được là: 53210 – 10235 = 42975
Đáp số: 42975.
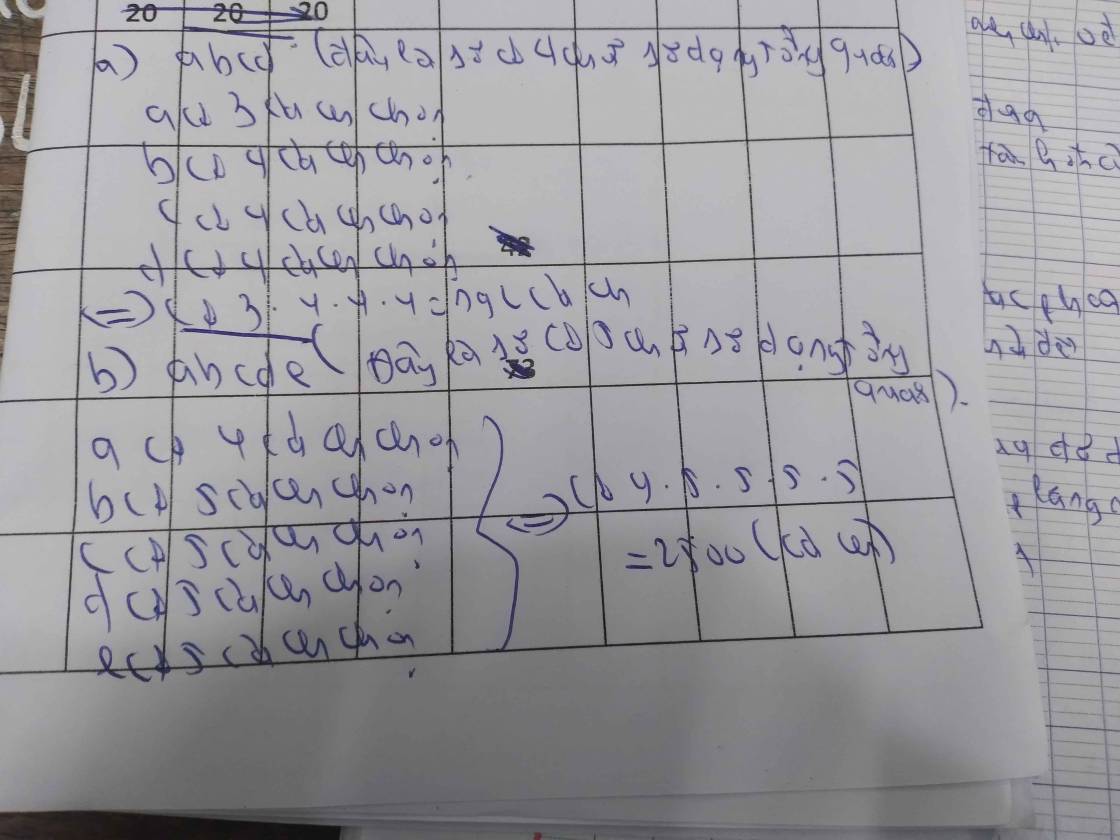
có 4 cách chọn chữ số hàng nghìn
3 cách chọn chữ số hàng trăm
2 cách chọn chữ số hàng chục
1 cách chọn chữ số hàng đơn vị
vậy có : 1 * 2 * 3 * 4 =24 số
Không thể lập được số nào
Vì số chia hết cho 5 phải có chữ số tận cùng là 0 và 5
4 chữ số phải là số chẵn nhưng 5 không phải số chẵn
Suy ra không thể lập được số nào