Giúp vs mk đag gấp lắm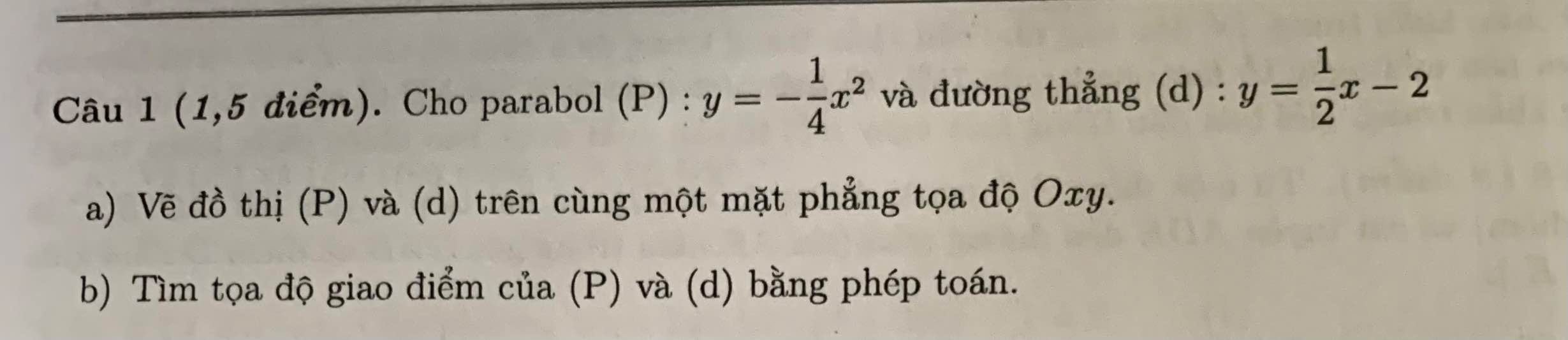
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
T
28 tháng 9 2018
a)\(\left(x+1\right)\left(x-5\right)< 0\) khi \(\left(x+1\right)\) và \(\left(x-5\right)\) trái dấu.
Chú ý rằng: \(x+1>x-5\) nên \(x+1>0,x-5< 0\). Giải cả hai trường hợp ta có:
\(\hept{\begin{cases}x+1>0\\x-5< 0\end{cases}\Leftrightarrow\hept{\begin{cases}x>-1\\x< 5\end{cases}}\Leftrightarrow-1< x< 5}\)
b) \(\left(x-2\right)\left(x+\frac{5}{7}\right)>0\) khi \(\left(x-2\right)\) và \(\left(x+\frac{5}{7}\right)\) đồng dấu (\(x-2\ne0,\left(x+\frac{5}{7}\right)\ne0\Leftrightarrow x\ne2;x\ne-\frac{5}{7}\)
+ Với \(\left(x-2\right)\) và \(\left(x+\frac{5}{7}\right)\) dương thì ta có:\(x-2< x+\frac{5}{7}\). Có 2 TH
\(\hept{\begin{cases}x-2>0\\x+\frac{5}{7}>0\end{cases}\Leftrightarrow\hept{\begin{cases}x>2\\x>-\frac{5}{7}\end{cases}}}\) . Dễ thấy để thỏa mãn cả hai trường hợp thì x > 2 (1)
+ Với \(\left(x-2\right)\) và \(\left(x+\frac{5}{7}\right)\) âm thì ta có: \(x-2< x+\frac{5}{7}\). Có 2 TH
\(\hept{\begin{cases}\left(x-2\right)< 0\\\left(x+\frac{5}{7}\right)< 0\end{cases}\Leftrightarrow\hept{\begin{cases}x< 2\\x< -\frac{5}{7}\end{cases}}}\). Dễ thấy để x thỏa mãn cả hai trường hợp thì \(x< -\frac{5}{7}\) (2)
Từ (1) và (2) ta có: \(\hept{\begin{cases}x>2\\x< -\frac{5}{7}\end{cases}}\) thì \(\left(x-2\right)\left(x+\frac{5}{7}\right)>0\)
3 tháng 3 2022
Dài qa nên jup 10 câu thoi nha =))
higher => highest
gives => gave
pleasing => pleased
lacing => to lace
quite so => bỏ quite
to turn on => turning on
would rather live on => would rather to live on
open for => open to
in => from
were => was
TG
12 tháng 12 2016
A D B C
5 dm = 50 cm
Tam giác ABC Và tam giác ABD có chung chiều cao nhận cạnh đáy BC
Chiều cao tam giác ABC :
150 : 50 = 3 cm
Đáy BC :
120 : 3 = 40 cm
16 tháng 2 2024
5 dm = 50 cm
Tam giác ABC Và tam giác ABD có chung chiều cao nhận cạnh đáy BC
Chiều cao tam giác ABC :150x2:50=6cm
bc là 120x2:6=40cm
TN
1
b.
Phương trình hoành độ giao điểm (P) và (d):
\(-\dfrac{1}{4}x^2=\dfrac{1}{2}x-2\Leftrightarrow x^2+2x-8=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+4\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=2\Rightarrow1=-1\\x=-4\Rightarrow y=-4\end{matrix}\right.\)
Vậy (P) và (d) cắt nhau tại 2 điểm có tọa độ là (2;-1) là (-4;-4)