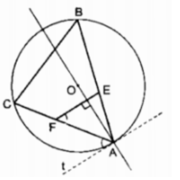
Trên đường tròn (O) đường kính AB = 2R (R > 0), lấy một điểm M bất kỳ (khác
A và B). Trên tia AB, lấy một điểm C sao cho AC = 3R, đường thẳng vuông góc với
AB tại C cắt đường thẳng AM tại E.
1. Chứng minh tứ giác BCEM nội tiếp trong một đường tròn.
2. Tính tích AM.AE theo R.
3. Lấy N là một điểm khác A, B, M nằm trên đường tròn (O), đường thẳng AN
cắt đường thẳng CE tại F. Chứng minh tứ giác MNFE nội tiếp trong một đường tròn.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo
https://asknlearn247.com/question/cho-duong-tron-o-r-duong-kinh-ab-co-dinh-tren-tia-doi-cua-tia-ab-lay-diem-c-sao-cho-ac-r-qua-c-k-2018212/
a, Xét (O), đường kính AB có: M ∈ (O)
⇒ ˆAMB=90°AMB^=90° (góc nội tiếp chắn nửa đường tròn)
⇒ AM ⊥ BP ⇒ ˆAMP=90°AMP^=90°
PC ⊥ AC (gt) ⇒ ˆACP=90°ACP^=90° Hay ˆBCP=90°BCP^=90°
Xét tứ giác ACPM có: ˆAMP+ˆACP=90°+90°=180°AMP^+ACP^=90°+90°=180°
Mà hai góc này ở vị trí đối nhau
⇒ Tứ giác ACPM nội tiếp đường tròn đường kính AP
b, Xét ΔBMA và ΔBCP có:
ˆBMA=ˆBCP=90°BMA^=BCP^=90°
ˆPBCPBC^: góc chung
⇒ ΔBMA ~ ΔBCP (g.g)
⇒ BMBC=BABPBMBC=BABP (các cặp cạnh tương ứng tỉ lệ)
⇒ BM.BP = BA.BC
Có BC=BA+CA=2R+R=3R
⇒ BM.BP=BA.BC=2R.3R=6R²
c, Tứ giác ACPM nội tiếp đường tròn đường kính AP (cmt)
⇒ ˆCPA=ˆCMACPA^=CMA^ (góc nội tiếp chắn CACA⏜)
Hay ˆCPQ=ˆCMACPQ^=CMA^
Xét (O) có: A, M, N, Q ∈ (O)
⇒ Tứ giác AMNQ nội tiếp (O)
⇒ ˆAQN+ˆAMN=180°AQN^+AMN^=180° (tổng hai góc đối trong tứ giác nội tiếp)
Mà ˆAMC+ˆAMN=180°AMC^+AMN^=180° (hai góc kề bù)
⇒ ˆAQN=ˆCMAAQN^=CMA^ Hay ˆPQN=ˆCMAPQN^=CMA^
Mà ˆCPQ=ˆCMACPQ^=CMA^ (cmt)
⇒ ˆCPQ=ˆPQNCPQ^=PQN^
Mà hai góc này ở vị trí so le trong so PQ cắt CP và NQ
⇒ CP // NQ
d, Gọi D là trung điểm của BC, kẻ đường thẳng qua Q song song với MO cắt AO tại I
Mà BC cố định ⇒ D cố định
Có O, D cố định ⇒ I cố định
Xét ΔMBC có: G là trọng tâm của ΔMBC (gt)
⇒ DGDM=13DGDM=13
Xét ΔOMD có: GI // MO (cách vẽ)
⇒ DGDM=GIMODGDM=GIMO (hệ quả định lí Talet)
⇒ GIMO=13⇒GI=MO3=R3GIMO=13⇒GI=MO3=R3
Mà R không đổi
⇒ G luôn cách I một khoảng bằng R3R3
⇒ Khi M di động, G luôn thuộc đường tròn tâm I, bán kính R3R3


1: góc AMB=1/2*180=90 độ
=>góc BME=90 độ
góc BCE+góc BME=90+90=180 độ
=>BMEC nội tiếp
2: Xét ΔAMB vuông tại M và ΔACE vuông tại C có
góc A chung
=>ΔAMB đồng dạng với ΔACE
=>AM/AC=AB/AE
=>AM*AE=AB*AC=6R^2
3: góc ANB=1/2*180=90 độ
Xét ΔANB vuông tại N và ΔACF vuông tại C có
góc BAN chung
=>ΔANB đồng dạng với ΔACF
=>AN/AC=AB/AF
=>AN*AF=AB*AC=AM*AE
=>AN/AE=AM/AF
=>ΔANM đồng dạng với ΔAEF
=>góc ANM=góc AEF
=>góc MEF+góc MNF=180 độ
=>MNFE nội tiếp