Cho tam giác ABC vuông tại A có AB = 6cm,AC = 8cm kẻ trung tuyến AM
a.Tính BC
b.Từ C kẻ đường thẳng vuông góc với AC cắt BM tại D.Chứng minh tam giác BAM = tam giác DCM
c.Chứng minh góc ABM > góc MBC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/ Xét tg vuông ABC có
BM=CM (gt) => AM=BM=CM=BC/2 (trong tg vuông trung tuyến thuộc cạnh huyền thì bằng nửa cạnh huyền)
=> tg ABM cân tại M => \(\widehat{BAM}=\widehat{ABM}\) (góc ở đáy tg cân)
b/ Xét tg vuông AEF và tg vuông AFM có
\(\widehat{AEF}=\widehat{FAM}\) (cùng phụ với \(\widehat{AFE}\) ) (1)
Mà AM=CM (cmt) => tg MAC cân tại M => \(\widehat{FAM}=\widehat{ACB}\) (góc ở đáy th cân) (2)
Từ (1) và (2) \(\Rightarrow\widehat{ACB}=\widehat{AEF}\)
Xét tg MBE và tg MFC có
\(\widehat{AEF}=\widehat{ACB}\) (cmt)
\(\widehat{BME}=\widehat{CMF}\) (góc đối đỉnh)
=> tg MBE đồng dạng với tg MFC (g.g.g)
c/ Xét tg vuông ABC và tg vuông AFE có
\(\widehat{AEF}=\widehat{ACB}\) (cmt)
=> tg ABC đông dạng với tg AFE
\(\Rightarrow\dfrac{AB}{AF}=\dfrac{AC}{AE}\Rightarrow AB.AE=AC.AF\)
d/

Bài 2
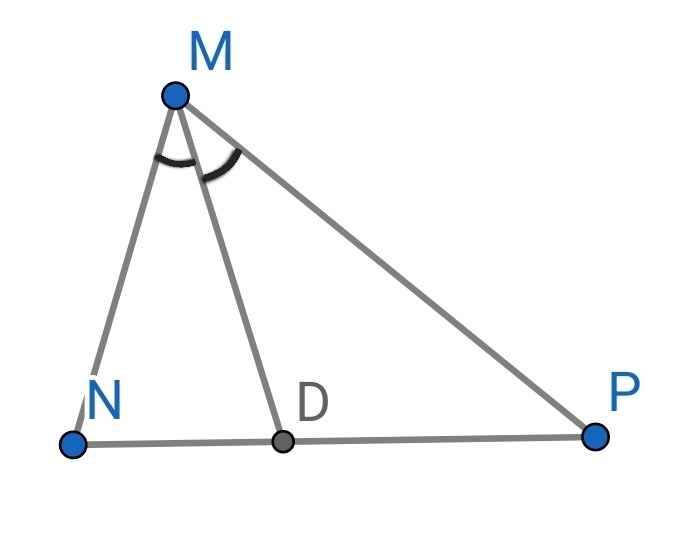
Ta có:
∠N + ∠DMN + ∠MDN = 180⁰ (tổng các góc trong ∆MDN)
⇒ ∠NMD = 180⁰ - (∠N + ∠MDN) (1)
∠P + ∠MDP + ∠PMD = 180⁰ (tổng các góc trong ∆MDP)
⇒ ∠PMD = 180⁰ - (∠MDP + ∠P) (2)
Do MD là tia phân giác của ∠NMP (gt)
⇒ ∠NMD = ∠PMD (3)
Từ (1), (2) và (3) ⇒ ∠DMP + ∠P = ∠N + ∠DMN
⇒ ∠DMP - ∠DMN = ∠N - ∠P
Bài 1
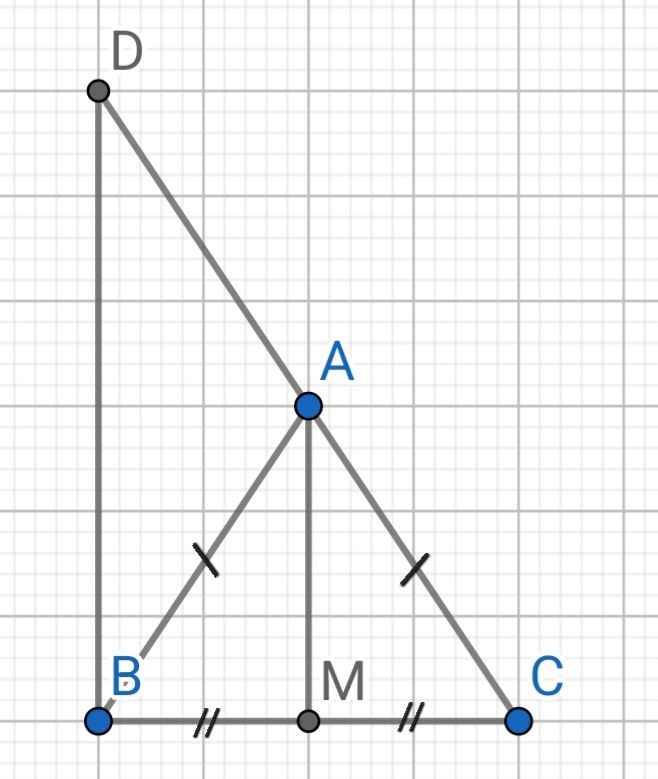 a) Do M là trung điểm của BC (gt)
a) Do M là trung điểm của BC (gt)
⇒ MB = MC
Xét ∆ABM và ∆ACM có:
AM là cạnh chung
AB = AC (gt)
MB = MC (cmt)
⇒ ∆ABM = ∆ACM (c-c-c)
b) Do ∆ABM = ∆ACM (cmt)
⇒ ∠AMB = ∠AMC (hai góc tương ứng)
Mà ∠AMB + ∠AMC = 180⁰ (kề bù)
⇒ ∠AMB = ∠AMC = 180⁰ : 2 = 90⁰
⇒ AM ⊥ BC
Mà BD ⊥ BC (gt)
⇒ BD // AM
c) Do ∆ABM = ∆ACM (cmt)
⇒ ∠BAM = ∠CAM (hai góc tương ứng)
Do BD // AM (cmt)
⇒ ∠ADB = ∠CAM (đồng vị)
∠ABD = ∠BAM (so le trong)
Mà ∠BAM = ∠CAM (cmt)
⇒ ∠ABD = ∠ADB

a.Áp dụng đl pytago:
BC^2 = AB^2 + AC^2
--> BC = 10 ( cm).
b. Xét góc CD vuông góc BD
AB vuoong góc BD
-- > BD vuông góc AC
-- > góc CDM= góc BAD ( so le trong)
Xét tam giác BAM và tam giác DCM có:
góc BMA = góc CMD ( đối đỉnh).
BM = MC ( AM là trung tuyến tam giác ABC).
góc CDM= góc BAD ( cmt)
do đó : tam giác BAM = tam giác DCM (g-c-g).
cảm ơn bn nhiều