trong mặt phẳng oxy cho tam giác abc với A(1;2),B(3;1),C(5;4)
a,viết PTTS,PTTQ của đường thằng AB
b,viết phương trình đường thẳng qua A và cách đều hai điểm B,C
c,tìm tọa độ hình chiếu của C trên đường thẳng AB
d,viết phương trình đường phân giác trong AD của tam giác ABC
e,viết phương trình đường tròn ngoại tiếp tam giác ABC
f,viết phương trình tiếp tuyến của đường tròn ngoại tiếp tam giác ABC tại A
g,viết phương trình đường tròn đi qua B,C và có tâm thuộc d;x+2y+3=0

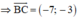
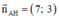 là VTPT là:
là VTPT là: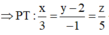
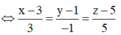
a: vecto AB=(2;-1)
PTTS AB là:
x=1+2t và y=2-t
vecto AB=(2;-1)
=>VTPT là (1;2)
PTTQ của AB là:
1(x-1)+2(y-2)=0
=>x-1+2y-4=0
=>x+2y-5=0
c:PT đường cao CH là:
2(x-5)+(-1)(y-4)=0
=>2x-10-y+4=0
=>2x-y-6=0
Tọa độ hình chiếu của C trên AB là:
2x-y-6=0 và x+2y-5=0
=>C(17/5;4/5)
e: PT (C) có dạng là:
x^2+y^2-2ax-2by+c=0
Theo đề, ta có:
1+4-2a-4b+c=0 và 9+1-6a-2b+c=0 và 25+16-10a-8b+c=0
=>a=23/8; b=13/4; c=55/4
=>(C): x^2+y^2-23/4x-13/2x+55/4=0
=>x^2-2*x*23/8+529/64+y^2-2*x*13/4+169/16=325/64
=>(x-23/8)^2+(y-13/4)^2=325/64