 ai giúp em vs ạ t5 em phải thi rồi ;-;
ai giúp em vs ạ t5 em phải thi rồi ;-;
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bổn phận của trẻ em : yêu thương ông bà , cha mẹ , anh chị em trong nhà ; lễ phép với ông bà , bố mẹ ; kính trọng ông bà và bố mẹ . Phải tỏ lòng biết ơn , Hiếu thảo đối với người đã có công to lớn của cuộc đời chúng ta .Giúp đỡ người khác khi gặp khó khăn ; yêu lớp , yêu trường . Kính trọng với thầy cô .
+ Bản thân em đã làm :
- Luôn " dạ " và " vâng " khi nói chuyện với ông bà , bố mẹ hay những người lớn tuổi hơn em
- Nói chuyện có đầu có đuôi , không được nói trống không .
- Hiếu thảo với ông , với bà , với bố mẹ .
- Đoàn kết cùng cả lớp , bạn bè.
- THƯỜNG XUYÊN GIÚP ĐỠ CÁC BẠN TRONG LỚP .
- Ngoài giúp đỡ bạn bè cần giúp đỡ những người kém may mắn .
- Anh chị em yêu thương nhau , đùm bọc lẫn nhau.
-........
Tham khảo:
Trẻ em có bổn phận sau đây: Yêu quý, kính trọng, hiếu thảo với ông bà, cha mẹ; kính trọng thầy giáo, cô giáo; lễ phép với người lớn, thương yêu em nhỏ, đoàn kết với bạn bè; giúp đỡ người già yếu, người khuyết tật, tàn tật, người gặp hoàn cảnh khó khăn theo khả năng của mình.


a: E thuộc Ox nên E(x;0)
O(0;0); M(4;1); E(x;0)
\(OM=\sqrt{\left(4-0\right)^2+\left(1-0\right)^2}=\sqrt{17}\)
\(OE=\sqrt{\left(x-0\right)^2+\left(0-0\right)^2}=\sqrt{x^2}=\left|x\right|\)
Để ΔOEM cân tại O thì OE=OM
=>\(\left|x\right|=\sqrt{17}\)
=>\(x=\pm\sqrt{17}\)

2.
Gọi \(H\left(x;y\right)\) là toạ độ chân đường cao ứng với BC \(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AH}=\left(x-1;y+2\right)\\\overrightarrow{BC}=\left(2;1\right)\end{matrix}\right.\)
Do AH vuông góc BC \(\Rightarrow\overrightarrow{AH}.\overrightarrow{BC}=0\)
\(\Rightarrow2\left(x-1\right)+y+2=0\Leftrightarrow y=-2x\)
\(\Rightarrow H\left(x;-2x\right)\Rightarrow\overrightarrow{BH}=\left(x+2;-2x-3\right)\)
Do H thuộc BC nên B, C, H thẳng hàng hay các vecto \(\overrightarrow{BC};\overrightarrow{BH}\) cùng phương
\(\Rightarrow\dfrac{x+2}{2}=\dfrac{-2x-3}{1}\Rightarrow x=\dfrac{8}{5}\Rightarrow y=-\dfrac{16}{5}\) \(\Rightarrow H\left(-\dfrac{8}{5};\dfrac{16}{5}\right)\)
\(\Rightarrow\overrightarrow{AH}=\left(-\dfrac{13}{5};\dfrac{26}{5}\right)\Rightarrow\left\{{}\begin{matrix}AH=\sqrt{\left(-\dfrac{13}{5}\right)^2+\left(-\dfrac{6}{5}\right)^2}=\dfrac{13\sqrt{5}}{5}\\BC=\sqrt{2^2+1^2}=\sqrt{5}\end{matrix}\right.\)
\(\Rightarrow S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{13}{2}\)
3.
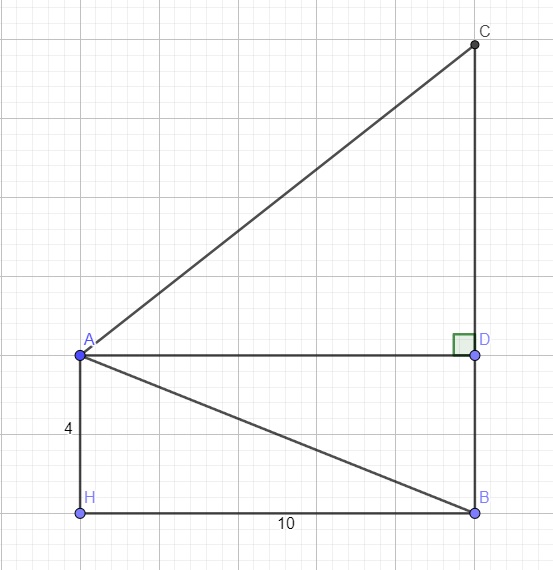
Kẻ AD vuông góc BC tại D
\(\Rightarrow AD=BH=10\) ; \(BD=AH=4\)
\(tan\widehat{BAD}=\dfrac{BD}{AD}=\dfrac{2}{5}\Rightarrow\widehat{BAD}\approx21^048'5''\)
\(\Rightarrow\widehat{CAD}=60^0-\widehat{BAD}=38^011'55''\)
\(\Rightarrow CD=AD.tan\widehat{CAD}=7,87\left(m\right)\)
\(\Rightarrow BC=BD+CD=11,87\left(m\right)\)