Bài 9 ạ giúp vs mn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(M=\sqrt{\dfrac{4}{\left(2-\sqrt{5}\right)^2}}-\sqrt{\dfrac{4}{\left(2+\sqrt{5}\right)^2}}=\dfrac{2}{\left|2-\sqrt{5}\right|}-\dfrac{2}{\left|2+\sqrt{5}\right|}\)
\(=\dfrac{2}{\sqrt{5}-2}-\dfrac{2}{\sqrt{5}+2}=\dfrac{2\left(\sqrt{5}+2\right)-2\left(\sqrt{5}-2\right)}{\left(\sqrt{5}-2\right)\left(\sqrt{5}+2\right)}\)
\(=\dfrac{8}{1}=8\)
Lm ơn giúp mik đii mà mik bt ơn bn đó nhiều lắm . Mik đang rất cần

THAM KHẢO
Gọi x là v.tốc dự định của xe(x>0, km/h)
Nửa quãng đường xe đi là: 120:2=60(km)
=> Vận tốc đi nửa quãng đường là: 60x60x (km/h)
=> Thời gian đi dự định là: 120x(h)120x(h)
Vì nửa qquangx đường sau xe đi với thời gian là: 60x+10(h)60x+10(h)
Theo bra ta có:
60x+60x+10=120x−0.560x+60x+10=120x−0.5
Gải được x=40(tmđk)
Vậy v.tốc dự định là 40km/h

a/ Tam giác AMN cân tại A (gt). \(\Rightarrow\) \(\widehat{AMN}=\widehat{ANM};AM=AN.\)
Xét tam giác AMB và tam giác ANC có:
+ AM = AN (cmt).
+ \(\widehat{AMB}=\widehat{ANC}\left(\widehat{AMN}=\widehat{ANM}\right).\)
+ MB = NC (gt).
\(\Rightarrow\) Tam giác AMB = Tam giác ANC (c - g - c).
\(\Rightarrow\) AB = AC (cặp cạnh tương ứng).
Xét tam giác ABC có: AB = AC (cmt).
\(\Rightarrow\) Tam giác ABC cân tại A.
b/ Tam giác ABC cân tại A (cmt) \(\Rightarrow\) \(\widehat{ABC}=\widehat{ACB}.\)
Mà \(\widehat{ABC}=\widehat{MBH;}\widehat{ACB}=\widehat{NCK}\text{}\) (đối đỉnh).
\(\Rightarrow\) \(\widehat{MBH}=\widehat{NCK}.\)
Xét tam giác MBH và tam giác NCK \(\left(\widehat{BHM}=\widehat{CKN}=90^o\right)\)có:
+ MB = NC (gt).
+ \(\widehat{MBH}=\widehat{NCK}\left(cmt\right).\)
\(\Rightarrow\) Tam giác MBH = Tam giác NCK (cạnh huyền - góc nhọn).
c/ Tam giác MBH = Tam giác NCK (cmt).
\(\Rightarrow\) \(\widehat{BMH}=\widehat{CNK}\) (cặp góc tương ứng).
Xét tam giác OMN có: \(\widehat{NMO}=\widehat{MNO}\) (do \(\widehat{BMH}=\widehat{CNK}\)).
\(\Rightarrow\) Tam giác OMN tại O.

Cách 1 :
Ta có : \(\frac{7}{11}=\frac{63}{99}\)
\(\frac{5}{9}=\frac{55}{99}\)
Vì 63 > 55 \(\Rightarrow\frac{63}{99}>\frac{55}{99}\)
Vậy \(\frac{7}{11}>\frac{5}{9}\)
Cách 2 :
Ta có :\(\frac{7}{11}=1-\frac{4}{11}\)
\(\frac{5}{9}=1-\frac{4}{9}\)
Vì \(\frac{4}{11}< \frac{4}{9}\Rightarrow\frac{7}{11}>\frac{5}{9}\)


c. \(\left|\dfrac{8}{4}-\left|x-\dfrac{1}{4}\right|\right|-\dfrac{1}{2}=\dfrac{3}{4}\)
\(\Rightarrow\left[{}\begin{matrix}\left|\dfrac{8}{4}-x+\dfrac{1}{4}\right|-\dfrac{1}{2}=\dfrac{3}{4}\\\left|\dfrac{8}{4}+x-\dfrac{1}{4}\right|-\dfrac{1}{2}=\dfrac{3}{4}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}\left|\dfrac{9}{4}-x\right|-\dfrac{1}{2}=\dfrac{3}{4}\\\left|\dfrac{7}{4}+x\right|-\dfrac{1}{2}=\dfrac{3}{4}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\left[{}\begin{matrix}\dfrac{9}{4}-x-\dfrac{1}{2}=\dfrac{3}{4}\\x=\dfrac{9}{4}-\dfrac{1}{2}=\dfrac{3}{4}\end{matrix}\right.\\\left[{}\begin{matrix}\dfrac{7}{4}+x-\dfrac{1}{2}=\dfrac{3}{4}\\-\dfrac{7}{4}-x-\dfrac{1}{2}=\dfrac{3}{4}\end{matrix}\right.\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}\left[{}\begin{matrix}x=1\\x=\dfrac{7}{2}\end{matrix}\right.\\\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=-3\end{matrix}\right.\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{7}{2}\\x=-3\end{matrix}\right.\)
Ở nơi x=9/4-1/2 là x-9/4-1/2 nha
a. -1,5 + 2x = 2,5
<=> 2x = 2,5 + 1,5
<=> 2x = 4
<=> x = 2
b. \(\dfrac{3}{2}\left(x+5\right)-\dfrac{1}{2}=\dfrac{4}{3}\)
<=> \(\dfrac{3}{2}x+\dfrac{15}{2}-\dfrac{1}{2}=\dfrac{4}{3}\)
<=> \(\dfrac{9x}{6}+\dfrac{45}{6}-\dfrac{3}{6}=\dfrac{8}{6}\)
<=> 9x + 45 - 3 = 8
<=> 9x = 8 + 3 - 45
<=> 9x = -34
<=> x = \(\dfrac{-34}{9}\)


`@` `\text {Ans}`
`\downarrow`
`1,`
`a)`
\(\dfrac{x}{2}=\dfrac{y}{3}\text{ và }x+y=50\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
`x/2 = y/3 = (x+y)/(2 + 3) = 50/5 = 10`
`=> x/2 = y/3 = 10`
`=> x = 10*2 = 20; y = 3*10 = 30`
Vậy, `x = 20; y = 30`
`b)`
\(\dfrac{x}{2}=\dfrac{y}{3}\text{ và }5x+4y=110\)
Ta có:
`x/2 = y/3` `=> (5x)/10 = (4y)/12`
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
`(5x)/10 = (4y)/12 = (5x+4y)/(10 + 12) = 110/22 = 5`
`=> x/2 = y/3 = 5`
`=> x = 2*5 = 10; y = 3*5 = 15`
Vậy, `x = 10; y = 15`
`c)`
\(5x=11y\text{ và }2x+3y=37\)
Ta có:
`5x = 11y -> x/11 = y/5 -> (2x)/22 = (3y)/15`
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
`(2x)/22 = (3y)/15 = (2x+3y)/(22+15) = 37/37 = 1`
`=> x/11 = y/5 = 1`
`=> x = 11; y = 5`
Vậy, `x = 11; y = 5`
`d)`
\(\dfrac{x}{2}=\dfrac{y}{1}\text{và }x+y-63=0\)
Ta có: `x + y - 63 = 0 -> x + y = 63`
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
`x/2 = y/1 = (x+y)/(2+1) = 63/3 = 21`
`=> x/2 = y/1 = 21`
`=> x = 21*2 =42; y = 21`
Vậy, `x = 42; y = 21.`
`2,`
`a)`
\(\dfrac{a}{14}=\dfrac{b}{2}=\dfrac{c}{4}\text{ và }a+b+c=5\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
`a/14 = b/2 = c/4 = (a+b+c)/(14+2+4)=5/20=1/4=0,25`
`=> a/14 = b/2 = c/4 = 0,25`
`=> a = 14*0,25 = 3,5` `; b = 2*0,25 = 0,5;` `c = 4*0,25 = 1`
Vậy, `a = 3,5`; `b = 0,5`; `c = 1`
`b)`
\(\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{c}{8}\text{ và }7a+3b-5c=7\)
Ta có:
`a/3 = b/5 = c/8 => (7a)/21 = (3b)/15 = (5c)/40`
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
`(7a)/21 = (3b)/15 = (5c)/40 = (7a + 3b - 5c)/(21 + 15 - 40)=7/-4 = -1,75`
`=> a/3 = b/5 = c/8 = -1,75`
`=> a = 3*(-1,75) = -5,25`
`b = 5*(-1,75) = -8,75`
`c = 8*(-1,75) = -14`
Vậy, `a = -5,25; b = -8,75`; `c = -14`
`c)`
\(\dfrac{a}{3}=\dfrac{b}{8}=\dfrac{c}{5}\text{và }3a+b-2c=14\)
Ta có:
`a/3 = b/8 = c/5 -> (3a)/9 = b/8 = (2c)/10`
Câu này bạn làm tương tự nha
`d)`
\(\dfrac{a}{3}=\dfrac{b}{2};\dfrac{b}{7}=\dfrac{c}{5}\text{ và }3a+5c-7b=30\)
Ta có:
`a/3 = b/2 -> a/21 = b/14`/
`b/7 = c/5 -> b/14 = c/10`
`=> a/21 = b/14 = c/10`
`=> (3a)/63 = (7b)/98 = (5c)/50`
Câu này bạn cũng làm tương tự.

Bài 1:
ĐKXĐ: $x>0; x\neq 1$
\(A=\frac{(\sqrt{x}-1)(x+\sqrt{x}+1)}{\sqrt{x}(\sqrt{x}-1)}-\frac{(\sqrt{x}+1)(x-\sqrt{x}+1)}{\sqrt{x}(\sqrt{x}+1)}+\frac{x+1}{\sqrt{x}}\)
\(=\frac{x+\sqrt{x}+1}{\sqrt{x}}-\frac{x-\sqrt{x}+1}{\sqrt{x}}+\frac{x+1}{\sqrt{x}}=\frac{x+\sqrt{x}+1-(x-\sqrt{x}+1)+(x+1)}{\sqrt{x}}\)
\(=\frac{x+2\sqrt{x}+1}{\sqrt{x}}=\frac{(\sqrt{x}+1)^2}{\sqrt{x}}\)
Bài 2:
\(\frac{x+2}{x\sqrt{x}+1}+\frac{\sqrt{x}-1}{x-\sqrt{x}+1}-\frac{\sqrt{x}-1}{x-1}\)
\(=\frac{x+2}{(\sqrt{x}+1)(x-\sqrt{x}+1)}+\frac{(\sqrt{x}-1)(\sqrt{x}+1)}{(\sqrt{x}+1)(x-\sqrt{x}+1)}-\frac{\sqrt{x}-1}{(\sqrt{x}-1)(\sqrt{x}+1)}\)
\(=\frac{x+2+x-1}{(\sqrt{x}+1)(x-\sqrt{x}+1)}-\frac{1}{\sqrt{x}+1}=\frac{2x+1}{(\sqrt{x}+1)(x-\sqrt{x}+1)}-\frac{x-\sqrt{x}+1}{(\sqrt{x}+1)(x-\sqrt{x}+1)}\)
\(=\frac{2x+1-(x-\sqrt{x}+1)}{(\sqrt{x}+1)(x-\sqrt{x}+1)}=\frac{x+\sqrt{x}}{(\sqrt{x}+1)(x-\sqrt{x}+1)}\)
\(=\frac{\sqrt{x}(\sqrt{x}+1)}{(\sqrt{x}+1)(x-\sqrt{x}+1)}=\frac{\sqrt{x}}{x-\sqrt{x}+1}\)
Theo BĐT Cô-si:
$x+1\geq 2\sqrt{x}\Rightarrow x-\sqrt{x}+1\geq \sqrt{x}$
$\Rightarrow B\leq \frac{\sqrt{x}}{\sqrt{x}}=1$
Dấu "=" xảy ra khi $x=1$ (không thỏa mãn vì $x\neq 1$)
$\Leftrightarrow B< 1$





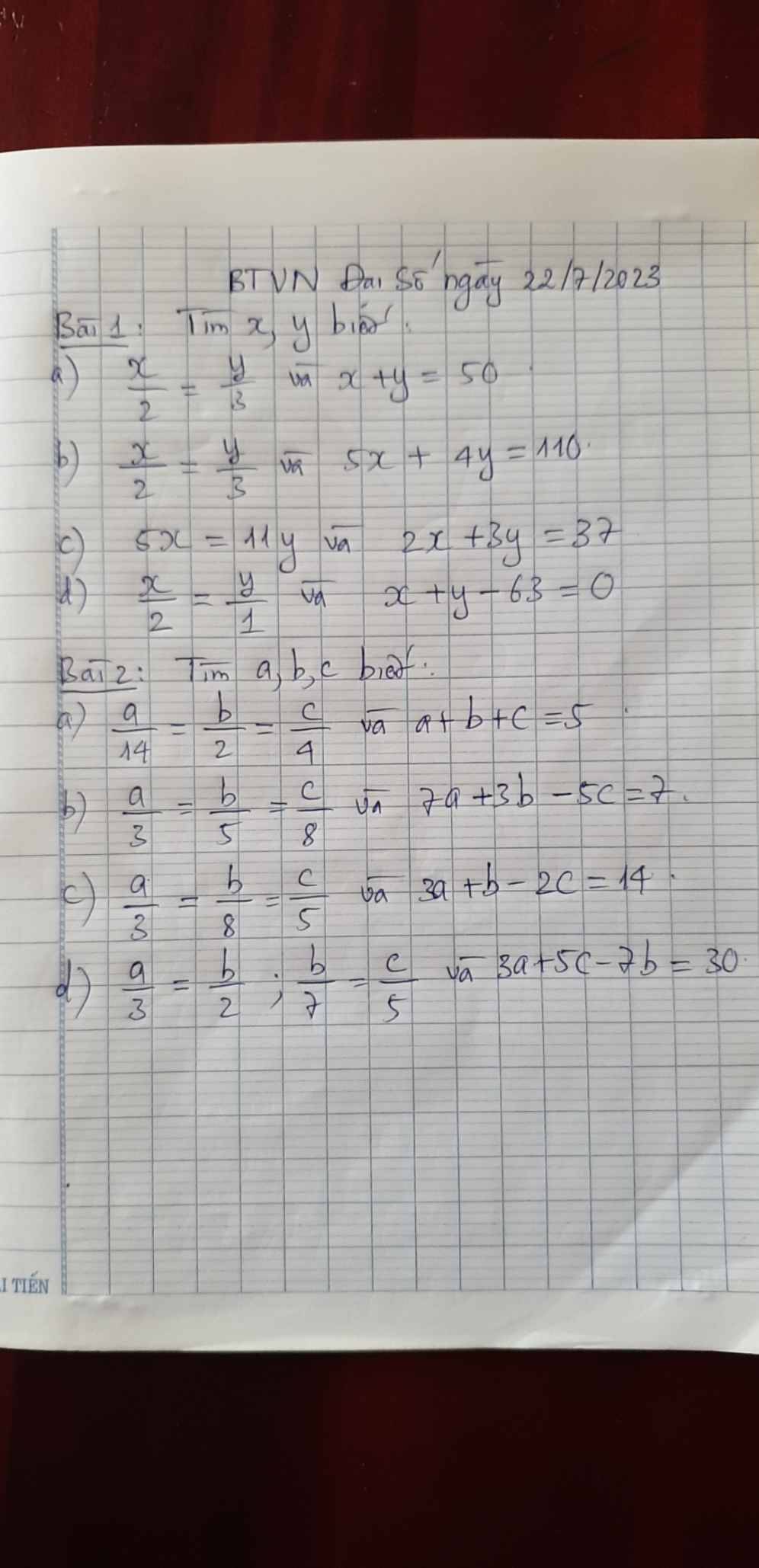
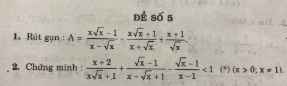 Mn giúp mình bài 2 vs ạ
Mn giúp mình bài 2 vs ạ