cho tam giác abc nhọn (ab ac) nội tiếp đường tròn hai đường cao BD và CE cắt nhau tại h đường ah cắc bc và đường trong tâm o lần lượt tại F và K
a) chứng minh tg BEDC nội tiếp
b) gọi I là hình chiếu của d lên AB c/m BD^2 = BI.BA
c) Gọi J là giao điểm của KD và đường tròn tâm o c/m góc BJK = góc BDE

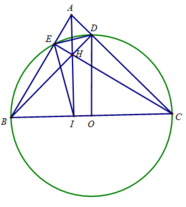

a: góc BEC=góc BDC=90 độ
=>BEDC nội tiếp
b: ΔADB vuông tại D có DI là đường cao
nên BD^2=BI*BA