các bạn giúp mìn cách tìm ra giá trị nhỏ nhất và giá trị lớn nhất
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


giá trị lớn nhất là:9999 + 9998 = 19997
giá trị nhỏ nhất là: (-9999) + (-9998)= -19997
nghĩ 3 năm mới ra:))

a) Có \(|x+3|\)\(\ge\)0
=>\(100-\)\(|x+3|\le100\)
=> GTLN của A là 100 khi x= -3
b) Tương tự GTNN của B là 100 khi x=2

uses crt;
var a:array[1..100]of integer;
n,i,k,max,min,t:integer;
begin
clrscr;
write('Nhap n='); readln(n);
for i:=1 to n do
begin
write('A[',i,']='); readln(a[i]);
end;
write('Nhap k='); readln(k);
max:=a[1];
for i:=1 to n do
if max<a[i] then max:=a[i];
writeln('Gia tri lon nhat la: ',max);
writeln('Vi tri la: ');
for i:=1 to n do
if max=a[i] then write(i:4);
writeln;
min:=a[1];
for i:=1 to n do
if min>a[i] then min:=a[i];
writeln('Gia tri nho nhat la: ',min);
writeln('Vi tri la: ');
for i:=1 to n do
if min=a[i] then write(i:4);
writeln;
t:=0;
for i:=1 to n do
if i mod 2=0 then t:=t+sqr(a[i]);
writeln('Tong binh phuong cac gia tri o vi tri chan la: ',t);
readln;
end.

\(T=x^2-xy+y^2\)
\(=\left(x^2-xy+\frac{y^2}{4}\right)+\frac{3y^2}{4}\)
\(=\left(x-\frac{y}{2}\right)^2+\frac{3y^2}{4}\)
\(\ge\frac{3y^2}{4}\)
\(\ge0\)
Dấu "=" xảy ra khi x=y=0

\(y=-5\cdot\dfrac{1-cos2x}{2}+12sin2x+7\)
\(=-\dfrac{5}{2}+\dfrac{5}{2}\cdot cos2x+12\cdot sin2x+7\)
\(=12\cdot sin2x+\dfrac{5}{2}\cdot cos2x+\dfrac{9}{2}\)
\(=\dfrac{\sqrt{601}}{2}\cdot\left(\dfrac{12\cdot sin2x}{\dfrac{\sqrt{601}}{2}}+cos2x\cdot\dfrac{5}{2}\cdot\dfrac{2}{\sqrt{601}}\right)+\dfrac{9}{2}\)
\(=\dfrac{\sqrt{601}}{2}\cdot\left(sin2x\cdot cosa+cos2x\cdot sina\right)+\dfrac{9}{2}\)
\(=\dfrac{\sqrt{601}}{2}\cdot sin\left(2x+a\right)+\dfrac{9}{2}\)
\(-1< =sin\left(2x+a\right)< =1\)
=>\(\dfrac{-\sqrt{601}}{2}< =\dfrac{\sqrt{601}}{2}\cdot sin\left(2x+a\right)< =\dfrac{\sqrt{601}}{2}\)
=>\(\dfrac{-\sqrt{601}+9}{2}< =y< =\dfrac{\sqrt{601}+9}{2}\)
\(y_{min}\) khi sin(2x+a)=-1
=>\(2x+a=-\dfrac{pi}{2}+k2pi\)
=>\(2x=-\dfrac{pi}{2}-a+k2pi\)
=>\(x=-\dfrac{pi}{4}-\dfrac{a}{2}+kpi\)
\(y_{max}\) khi sin(2x+a)=1
=>\(2x+a=\dfrac{pi}{2}+k2pi\)
=>\(x=\dfrac{pi}{4}-\dfrac{a}{2}+kpi\)
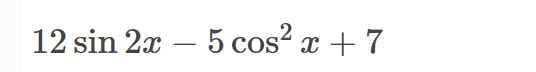
ban cho mình biết đề đi
mình cần cách làm á chứ mình k có đề cụ thể