Thực hiện phép tính: có lời giải chi...
Đọc tiếp
Thực hiện phép tính: 
có lời giải chi tiết
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LU
0
L
0
LN
1
H9
HT.Phong (9A5)
CTVHS
2 tháng 8 2023
\(\left(5^{19}\cdot5^{14}\right):5^{32}\)
\(=5^{19+14}:5^{32}\)
\(=5^{33}:5^{32}\)
\(=5^{33-32}\)
\(=5\)
27 tháng 12 2015
a) 59 . 73 - 302 +27 . 59
=59x(73+27)-302
=59x100-302
=5900-900
=5000
b) 1560 : [5 . 79 -( 125 + 5. 49) + 5. 21]
=1560:[5.79-(125+245)+5.21)
=1560:[5.(79+21)-(125+245)
=1560:[500-370]
=1560:130
=12
PP
1
25 tháng 11 2023
13: \(\left(-15\right)+8+7\)
\(=\left(-15\right)+\left(8+7\right)\)
=-15+15
=0
14: \(\left(-8\right)+2+6\)
\(=\left(-8\right)+\left(2+6\right)\)
=-8+8
=0
15: \(\left(-1\right)+3-2\)
\(=\left(-1-2\right)+3\)
=-3+3
=0
16: \(25-8-7\)
\(=25-\left(8+7\right)\)
=25-15
=10
17: \(8-2-6\)
\(=8-\left(2+6\right)\)
=8-8
=0
18: \(\left(-12\right)-3+15\)
\(=\left(-12-3\right)+15\)
=-15+15
=0
H
18 tháng 12 2022
\(a,2x^2+6x=2x\left(x+3\right)\\ b,x^2+2xy+y^2-9z^2\\ =\left(x^2+2xy+y^2\right)-\left(3z\right)^2\\ =\left(x+y\right)^2-\left(3z\right)^2\\ =\left(x+y-3z\right)\left(x+y+3z\right)\\ b,x^3-2x^2+x\\ =x\left(x^2+2x+1\right)\\ =x\left(x+1\right)^2\\ d,x^2-2x-15=x^2-5x+3x-15\\ =x\left(x-5\right)+3\left(x-5\right)\\ =\left(x+3\right)\left(x-5\right)\)
2 tháng 7 2021
Chủ yếu em phân tích sao cho có nhân tử chung ra là được
AT
2 tháng 7 2021
a) \(\sqrt{5}-\sqrt{48}+5\sqrt{27}-\sqrt{45}=\sqrt{5}-\sqrt{16.3}+5\sqrt{9.3}-\sqrt{9.5}\)
\(=\sqrt{5}-4\sqrt{3}+15\sqrt{3}-3\sqrt{5}=11\sqrt{3}-2\sqrt{5}\)
b) \(2\sqrt{3}+\sqrt{48}-\sqrt{75}-\sqrt{243}=2\sqrt{3}+\sqrt{16.3}-\sqrt{25.3}-\sqrt{81.3}\)
\(=2\sqrt{3}+4\sqrt{3}-5\sqrt{3}-9\sqrt{3}=-8\sqrt{3}\)
c) \(3\sqrt{50}-2\sqrt{75}-4\dfrac{\sqrt{54}}{\sqrt{3}}-3\sqrt{\dfrac{1}{3}}\)
\(=3\sqrt{25.2}-2\sqrt{25.3}-4\sqrt{\dfrac{54}{3}}-\sqrt{9.\dfrac{1}{3}}=15\sqrt{2}-10\sqrt{3}-4\sqrt{18}-\sqrt{3}\)
\(=15\sqrt{2}-11\sqrt{3}-4\sqrt{9.2}=15\sqrt{2}-11\sqrt{3}-12\sqrt{2}=3\sqrt{2}-11\sqrt{3}\)
mấy câu dưới bạn làm tương tự thôi
TK
2 tháng 7 2021
n)\(\dfrac{15}{\sqrt{6}+1}+\dfrac{4}{\sqrt{6}-2}-\dfrac{12}{3-\sqrt{6}}-\sqrt{\dfrac{1}{6}}\)
=\(\dfrac{15\left(\sqrt{6}-1\right)}{\left(\sqrt{6}+1\right)\left(\sqrt{6}-1\right)}+\dfrac{4\left(\sqrt{6}+2\right)}{\left(\sqrt{6}-2\right)\left(\sqrt{6}+2\right)}-\dfrac{12\left(3+\sqrt{6}\right)}{\left(3-\sqrt{6}\right)\left(3+\sqrt{6}\right)}-\sqrt{\dfrac{1}{6}}\)
=\(\dfrac{15\left(\sqrt{6}-1\right)}{5}+\dfrac{4\left(\sqrt{6}+2\right)}{2}-\dfrac{12\left(3+\sqrt{6}\right)}{3}-\sqrt{\dfrac{1}{6}}\)
=\(3\left(\sqrt{6}-1\right)+2\left(\sqrt{6}+2\right)-4\left(3+\sqrt{6}\right)-\sqrt{\dfrac{1}{6}}\)
=\(3\sqrt{6}-3+2\sqrt{6}+4-12-4\sqrt{6}-\sqrt{\dfrac{1}{6}}\)
=\(\sqrt{6}-11-\sqrt{\dfrac{1}{6}}\)
=\(\dfrac{5-11\sqrt{6}}{\sqrt{6}}\)
TK
2 tháng 7 2021
h)\(\sqrt{\left(\sqrt{3}-3\right)^2}+\sqrt{4-2\sqrt{3}}\)
=\(\left|\sqrt{3}-3\right|+\sqrt{3-2\sqrt{3}+1}\)
=\(3-\sqrt{3}+\sqrt{\left(\sqrt{3}-1\right)^2}\)
=\(3-\sqrt{3}+\left|\sqrt{3}-1\right|\)
=\(3-\sqrt{3}+\sqrt{3}-1\)
=2
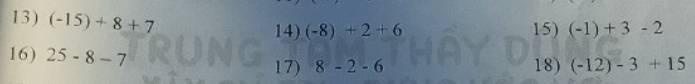
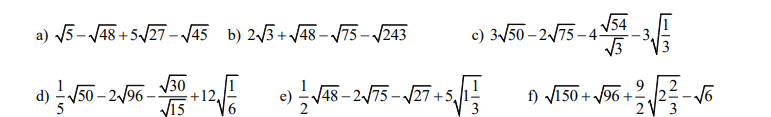
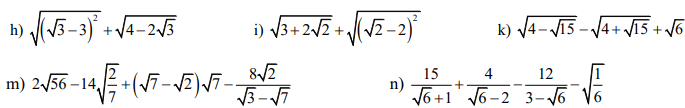
\(\dfrac{-8}{3}\)