Tính tổng S= -1-1/2-1/4-1/8-1/16-......-1/1024
Giúp mik nha.Mình tick cho !!!!!!!!!!!!!!!!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
22 tháng 7 2023
1/
\(N=1.\left(2-1\right)+2\left(3-1\right)+3\left(4-1\right)+...+99\left(100-1\right)=\)
\(=\left(1.2+2.3+3.4+...+99.100\right)-\left(1+2+3+...+99\right)=\)
Đặt
\(A=1.2+2.3+3.4+...+99.100\)
\(3A=1.2.3+2.3.3+3.4.3+...+99.100.3=\)
\(=1.2.3+2.3.\left(4-1\right)+3.4.\left(5-2\right)+...+99.100.\left(101-98\right)=\)
\(=1.2.3-1.2.3+2.3.4-2.3.4+3.4.5-...-98.99.100+99.100.101=\)
\(=99.100.101\Rightarrow A=\dfrac{99.100.101}{3}=33.100.101\)
Đặt
\(B=1+2+3+...+99=\dfrac{99.\left(1+99\right)}{2}=4950\)
\(\Rightarrow N=A-B\)
2/
Số hạng cuối cùng là 10000 hoặc 1000000 mới làm được
\(A=1^2+2^2+3^2+...+100^2\)
Tính như câu 1
3/ Làm như bài 4
4/
\(S=1^2+3^2+5^2+...+99^2=\)
\(=1.\left(3-2\right)+3\left(5-2\right)+5\left(7-2\right)+...+99\left(101-2\right)=\)
\(=\left(1.3+3.5+5.7+...+99.101\right)-2\left(1+3+5+...+99\right)\)
Đặt
\(B=1+3+5+...+99=\dfrac{50.\left(1+99\right)}{2}=2500\)
Đặt
\(A=1.3+3.5+5.7+...+99.101\)
\(6A=1.3.6+3.5.6+3.7.6+...+99.101.6=\)
\(=1.3.\left(5+1\right)+3.5.\left(7-1\right)+5.7.\left(9-3\right)+...+99.101.\left(103-97\right)=\)
\(=1.3+1.3.5-1.3.5+3.5.7-3.5.7+5.7.9-...-97.99.101+99.101.103=\)
\(=3+99.101.103\Rightarrow A=\dfrac{3+99.101.103}{6}\)
\(\Rightarrow S=A-2B\)
GH
Gia Hân
VIP
22 tháng 7 2023
Bài 1:
\(N=1^2+2^2+3^3+...+99^2\)
\(N=1.1+2.2+3.3+...+99.99\)
\(N=1.\left(2-1\right)+2.\left(3-1\right)+3.\left(4-1\right)+...+99.\left(100-1\right)\)
\(N=1.2-1+2.3-2+3.4-3+...+99.100-99\)
\(N=\left(1.2+2.3+3.4+...+99.100\right)-\left(1+2+3+...+99\right)\)
Đặt \(\left\{{}\begin{matrix}A=1.2+2.3+3.4+...+99.100\\B=1+2+3+...+99\end{matrix}\right.\)
+) Tính \(A=1.2+2.3+3.4+...+99.100\)
Ta có:
\(3A=1.2.3+2.3.3+3.4.3+...+99.100.3\)
\(3A=1.2.3+2.3.\left(4-1\right)+3.4.\left(5-2\right)+...+99.100.\left(101-98\right)\)
\(3A=1.2.3+2.3.4-1.2.3+3.4.5-2.3.4+...+99.100.101-98.99.100\)
\(3A=99.100.101\)
\(\Rightarrow A=\dfrac{99.100.101}{3}=333300\)
+) Tính \(B=1+2+3+...+99\)
\(B\) có số số hạng là: \(\dfrac{99-1}{1}\) + 1 = 99 (số hạng)
\(\Rightarrow B=\dfrac{\left(99+1\right).99}{2}=4950\)
\(\Rightarrow N=A-B=333300-4950=328350\)
\(\Rightarrow N=328350\)
CM
24 tháng 6 2017
Cộng thêm 1/2 vào biểu thức đã cho, có:
S + 1/2= 1/2+1/4+ 1/8+ 1/16+1/32+1/64+1/128
Nhận xét:
TT
1
12 tháng 3 2018
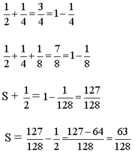
BÀI 1:
\(S=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}\)
\(S=1+\frac{1}{1.2}+\frac{1}{2.2}+\frac{1}{2.4}+\frac{1}{4.4}+\frac{1}{4.8}\)
\(S=1+1-\frac{1}{2}+\frac{1}{2}-\frac{1}{2}+\frac{1}{2}-\frac{1}{4}+\frac{1}{4}-\frac{1}{4}+\frac{1}{4}-\frac{1}{8}\)
\(S=1+1-\frac{1}{8}\)
\(S=\frac{15}{8}\)
BÀI 2:
\(A=1.2+2.3+3.4+...+98.99\)
\(\Rightarrow3A=1.2.3+2.3.3+3.4.3+...+98.99.3\)
\(3A=1.2.\left(3-0\right)+2.3.\left(4-1\right)+3.4.\left(5-2\right)+...+98.99.\left(100-97\right)\)
\(3A=1.2.3+2.3.4-1.2.3+3.4.5-2.3.4+...+98.99.100-97.98.99\)
\(3A=\left(1.2.3+2.3.4+3.4.5+98.99.100\right)-\left(1.2.3+2.3.4+...+97.98.99\right)\)
\(3A=98.99.100\)
\(3A=970200\)
\(\Rightarrow A=970200:3\)
\(A=323400\)
CHÚC BN HỌC TỐT!!!
13 tháng 8 2018
Xét TH1 : ( S < 8/9 )
\(\frac{1}{2\cdot2}< \frac{1}{1\cdot2};\frac{1}{3\cdot3}< \frac{1}{2\cdot3};...;\frac{1}{9\cdot9}< \frac{1}{8\cdot9}\)
\(\Rightarrow\frac{1}{2^2}+\frac{1}{3^2}+...+\frac{1}{9^2}< \frac{1}{1\cdot2}+\frac{1}{2\cdot3}+...+\frac{1}{8\cdot9}\)
hay \(S< \frac{1}{1\cdot2}+\frac{1}{2\cdot3}+...+\frac{1}{8\cdot9}\)
\(S< 1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{8}-\frac{1}{9}\)
\(S< 1-\frac{1}{9}=\frac{8}{9}\left(1\right)\)
TH2 : ( S > 2/5 )
\(\frac{1}{2\cdot2}>\frac{1}{2\cdot3};\frac{1}{3\cdot3}>\frac{1}{3\cdot4};...;\frac{1}{9\cdot9}>\frac{1}{9\cdot10}\)
\(\Rightarrow\frac{1}{2^2}+\frac{1}{3^2}+...+\frac{1}{9^2}>\frac{1}{2\cdot3}+\frac{1}{3\cdot4}+...+\frac{1}{9\cdot10}\)
hay \(S>\frac{1}{2\cdot3}+\frac{1}{3\cdot4}+...+\frac{1}{9\cdot10}\)
\(S>\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{9}-\frac{1}{10}\)
\(S>\frac{1}{2}-\frac{1}{10}=\frac{2}{5}\left(2\right)\)
Từ (1) và (2) => đpcm
Ko tk thì ko phải là ng` nx rồi :)
23 tháng 1 2017
a)
Vì 2/9=6/27=8/36=12/54=16/72=18/81 nên:
2/9+6/27+8/36+12/54+16/72+18/81=
2/9+2/9+2/9+2/9+2/9+2/9=
2/9*6=
12/9=
4/3
Vậy 2/9+6/27+8/36+12/54+16/72+18/81=4/3
b)
Ta có:
1-2/5=3/5
1-2/7=5/7
1-2/9=7/9
...
1-2/99=97/99
Vậy (1-2/5)*(1-2/7)*(1-2/9)*...*(1-2/99)=
3/5*5/7*7/9*...*97/99=
(3*5*7*...*97)/(5*7*9*...*99)=
3/99=
1/33
Vậy (1-2/5)*(1-2/7)*(1-2/9)*...*(1-2/99)=1/33
c)
Gọi biểu thức 1/2+1/4+1/8+1/16+...+1/1024 là S,ta có:
S=1/2+1/4+1/8+1/16+...+1/1024
S*2=1+1/2+1/4+1/8+...+1/512
S*2-S=(1+1/2+1/4+1/8+...+1/512)-(1/2+1/4+1/8+1/16+...+1/1024)
S=1-1/1024
S=1023/1024
Vậy 1/2+1/4+1/8+1/16+...+1/1024=1023/1024
22 tháng 10 2016
S=1/2+1/4+1/8+1/16+1/32+1/64
S=1-1/2+1/2-1/4+1/4-1/8+1/8-1/16+1/16-1/32+1/32-1/64
S=1-1/64
S=63/64