Tìm các giá trị của x và y sao cho xy+=3x+2y
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AD
10 tháng 5 2022
|3x-2y| ≥ 0
|2z-5y| ≥ 0
|xy+yz+zx-174| ≥ 0
=> |3x-2y|+|2z-5y|+|xy+yz+zx-174| ≥ 0
=> p ≥ 2017
vậy GTNN của p là 2017
7 tháng 1 2024
a: C=A-B
\(=5x^3+y^3-3x^2y+4xy^2-4x^3+6x^2y-xy^2\)
\(=x^3+3x^2y+3xy^2+y^3\)
D=A+B
\(=5x^3+y^3-3x^2y+4xy^2+4x^3-6x^2y+xy^2\)
\(=9x^3-9x^2y+5xy^2+y^3\)
bậc của C là 3
bậc của D là 3
b: Thay x=0 và y=-2 vào D, ta được:
\(D=9\cdot0^3-9\cdot0^2\left(-2\right)+5\cdot0\cdot\left(-2\right)^2+\left(-2\right)^3\)
\(=0-0+0-8=-8\)
c: Thay x=-1 và y=-1 vào C, ta được:
\(C=\left(-1\right)^3+3\cdot\left(-1\right)^2\cdot\left(-1\right)+3\cdot\left(-1\right)\cdot\left(-1\right)^2+\left(-1\right)^3\)
=-8
CM
6 tháng 2 2019
Đáp án C
Phương pháp:
- Sử dụng tính đơn điệu của hàm số để giải phương trình, từ đó đánh giá giá trị lớn nhất của biểu thức.
Cách giải:
<=> 
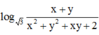
(2)
Đặt 
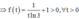
=> f(t) đồng biến trên (0;+∞)
<=> 
<=> 
Khi đó,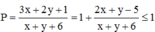 
vì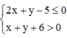 
Vậy Pmax = 1 khi và chỉ khi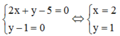 
CM
13 tháng 9 2019
Đáp án C
Phương pháp giải:
- Sử dụng tính đơn điệu của hàm số để giải phương trình, từ đó đánh giá giá trị lớn nhất của biểu thức.
Lời giải:
log 3 x + y x 2 + y 2 + x y + 2 = x ( x - 3 ) + y ( y - 3 ) + x y (1)
(2)
Đặt 
=> f(t) đồng biến trên (0;+∞)
Khi đó, 
vì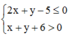 
Vậy Pmax = 1 khi và chỉ khi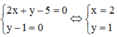 
13 tháng 2 2022
\(P=\dfrac{1}{3}x^2y+xy^2-xy+\dfrac{1}{2}xy^2-5xy-\dfrac{1}{3}x^2y=\dfrac{3}{2}xy^2-6xy\)
Thay x = 2 ; y = 1 ta được
\(\dfrac{3}{2}.2.1-6.2.1=3-12=-9\)
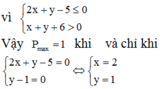
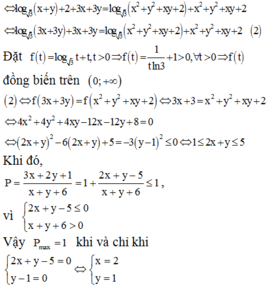
3x+7=28
3x =28-7
3x =21
x =21:3
x =7