giúp mình câu b ạ, cả câu c thì càng tốt
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(A=\dfrac{2^{13}\cdot3^7}{2^{15}\cdot3^2\cdot9^2}=\dfrac{2^{13}\cdot3^7}{2^{15}\cdot3^6}=\dfrac{3}{4}\)
\(C=27\cdot\left(-\dfrac{3}{2}\right)^{-5}\cdot\left(-\dfrac{2}{5}\right)^{-4}:\left(\dfrac{2}{125}\right)^{-1}\)
\(=27\cdot\dfrac{-32}{243}\cdot\dfrac{625}{16}\cdot\dfrac{2}{125}\)
\(=\dfrac{-32}{9}\cdot\dfrac{1}{8}\cdot5\)
\(=-\dfrac{20}{9}\)

Cách làm nói chung:
- Tìm vecto chỉ phương \(\overrightarrow{u}\) của đường d và vtpt \(\overrightarrow{n}\) của mặt (P)
- Tính tích có hướng \(\overrightarrow{u_1}=\left(\overrightarrow{u};\overrightarrow{n}\right)\)
- Tiếp tục tính tích có hướng \(\overrightarrow{u_2}=\left[\overrightarrow{u_1};\overrightarrow{n}\right]\)
- Tìm tọa độ giao điểm M của d và (P)
- Hình chiếu vuông góc của d lên (P) sẽ đi qua M và nhận \(\overrightarrow{u_2}\) (hoặc 1 vecto cùng phương với nó) là 1 vtcp
Lưu ý rằng có vô số cách viết 1 pt đường thẳng (tùy thuộc cách chọn điểm) nên có thể trong 4 đáp án của đề bài không đáp án nào giống pt vừa viết được. Lúc đó cần kiểm tra bằng cách: 1. Loại những đáp án không giống vecto chỉ phương. 2. Trong những đáp án còn lại, tìm 1 điểm trên đó và thay vào pt đường thẳng vừa viết được, nếu thỏa mãn thì đó là đáp án đúng.
1209.
d nhận \(\overrightarrow{u}=\left(1;1;-1\right)\) là 1 vtcp
(P) nhận \(\overrightarrow{n}=\left(1;2;1\right)\) là 1 vtpt
Ta có: \(\overrightarrow{u_1}=\left[\overrightarrow{u};\overrightarrow{n}\right]=\left(3;-2;1\right)\)
\(\overrightarrow{u_2}=\left[\overrightarrow{u_1};\overrightarrow{n}\right]=\left(-4;-2;8\right)=-2\left(2;1;-4\right)\)
Phương trình d dạng tham số: \(\left\{{}\begin{matrix}x=t\\y=1+t\\z=2-t\end{matrix}\right.\)
Gọi M là giao điểm d và (P), tọa độ M thỏa mãn:
\(t+2\left(1+t\right)+2-t-4=0\Rightarrow t=0\Rightarrow M\left(0;1;2\right)\)
Do đó hình chiếu của d lên (P) nhận (2;1;-4) là 1 vtcp và đi qua M(0;1;2)
Phương trình: \(\dfrac{x}{2}=\dfrac{y-1}{1}=\dfrac{z-2}{-4}\)
Câu 1210 hoàn toàn tương tự

a: \(=\dfrac{-\dfrac{1}{2}\left[cos\left(a+b+a-b\right)-cos\left(a+b-a+b\right)\right]}{cos^2b-cos^2a}\)
\(=\dfrac{-\dfrac{1}{2}\cdot\left[cos2a-cos2b\right]}{\dfrac{1-cos2b}{2}-\dfrac{1-cos2a}{2}}\)
\(=\dfrac{-\dfrac{1}{2}\cdot\left(cos2a-cos2b\right)}{\dfrac{1-cos2b-1+cos2a}{2}}=\dfrac{-\dfrac{1}{2}\cdot\left(cos2a-cos2b\right)}{\dfrac{1}{2}\cdot\left(cos2a-cos2b\right)}=-1\)
c: \(T=\dfrac{sina+sinb\cdot\left(cosa\cdot cosb-sina\cdot sinb\right)}{cosa-sinb\cdot\left(sina\cdot cosb+sinb\cdot cosa\right)}-tan\left(a+b\right)\)
\(=\dfrac{sina+sinb\cdot cosa\cdot cosb-sin^2b\cdot sina}{cosa-sinb\cdot sina\cdot cosb-sin^2b\cdot cosa}-tan\left(a+b\right)\)
\(=\dfrac{sina\left(1-sin^2b\right)+sinb\cdot cosa\cdot cosb}{cosa\left(1-sin^2b\right)-sinb\cdot sina\cdot cosb}\)-tan(a+b)
\(=\dfrac{sina\cdot cos^2b+sinb\cdot cosa\cdot cosb}{cosa\cdot cos^2b-sinb\cdot sina\cdot cosb}-tan\left(a+b\right)\)
\(=\dfrac{sina\cdot cosb+sinb\cdot cosa}{cosa\cdot cosb-sina\cdot sinb}-tan\left(a+b\right)\)
\(=\dfrac{sin\left(a+b\right)}{cos\left(a+b\right)}-tan\left(a+b\right)=0\)

c: Ta có: \(\left(\dfrac{1}{2}\right)^{2x+1}=\dfrac{1}{8}\)
\(\Leftrightarrow2x+1=3\)
\(\Leftrightarrow2x=2\)
hay x=1
d: Ta có: \(\left(-\dfrac{1}{3}\right)^{x+3}=\dfrac{1}{81}\)
\(\Leftrightarrow x+3=4\)
hay x=1

Bài 4
a, Số nu của gen là 90 x 20 = 1800 ( nu )
=> Chiều dài của gen \(\dfrac{1800}{2}.3,4=3060\left(A^O\right)\)
b,
Số nu của cả gen A=T=1800.20% = 360 (nu)
G=X=1800.30% = 540(nu)
Số nu từng mạch :
A1 = T2 = 15% . 900 = 135 ( nu )
T1 = A2 = 360 - 135 = 225 ( nu )
G1 = X2 = 540 - X1 = 540 - 360 = 180 ( nu )
X1 = G2 = 40% . 900 = 360 ( nu )
Bài 5
Ta có : \(\left\{{}\begin{matrix}H=2A+3G=N+G=3900\\G=900\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}A=T=600\left(nu\right)\\G=X=900\left(nu\right)\\N=3000,N1=N2=1500\left(nu\right)\end{matrix}\right.\)
A1 = T2 = 30%.1500= 450 (nu)
T1 = A2 = 600 - 450 = 150 (nu)
G1 = X2 = 10%.1500 = 150 ( nu )
G2 = X1 = 900 - 150 = 750 (nu)

\(7,x^4+x^3+x^2-1=x^3\left(x+1\right)+\left(x-1\right)\left(x+1\right)=\left(x^3+x-1\right)\left(x+1\right)\)
\(8,x^2y^2+1-x^2-y^2=\left(x^2y^2-y^2\right)-\left(x^2-1\right)\\ =y^2\left(x^2-1\right)-\left(x^2-1\right)=\left(x-1\right)\left(x+1\right)\left(y-1\right)\left(y+1\right)\)
\(10,x^4-x^2+2x-1=x^4-\left(x-1\right)^2=\left(x^2-x+1\right)\left(x^2+x-1\right)\\ 11,3a-3b+a^2-2ab+b^2=3\left(a-b\right)+\left(a-b\right)^2=\left(3+a-b\right)\left(a-b\right)\\ 12,a^2+2ab+b^2-2a-2b+1=\left(a+b\right)^2-2\left(a+b\right)+1=\left(a+b-1\right)^2\\ 13,a^2-b^2-4a+4b=\left(a-b\right)\left(a+b\right)-4\left(a-b\right)=\left(a+b-4\right)\left(a-b\right)\\ 14,a^3-b^3-3a+3b=\left(a-b\right)\left(a^2+ab+b^2\right)-3\left(a-b\right)=\left(a-b\right)\left(a^2+ab+b^2-3\right)\\ 15,x^3+3x^2-3x-1=\left(x-1\right)\left(x^2+x+1\right)+3x\left(x-1\right)=\left(x-1\right)\left(x^2+4x+1\right)\)
1)
=0,25y.(64x3+z3)
2)
=x2(x2-4x+4)
=x2(x-2)2
5)
=x2(x+1)-4(x+1)
=(x2-4)(x+1)
=(x-2)(x+2)(x+1)
6)
=x2(x-1)-(x-1)
=(x2-1)(x-1)
=(x-1)(x+1)(x-1)
=(x-1)2(x+1)

7.
Phương trình đường tròn \(\left(x-a\right)^2+\left(y-b\right)^2=R^2\) với tâm \(I=\left(a;b\right)\), bán kính \(R\)
\(\Rightarrow\) Tâm đường tròn \(\left(x-1\right)^2+\left(y+2\right)^2=4\) có tọa độ \(\left(1;-2\right)\)
Kết luận: Tâm đường tròn có tọa độ \(\left(1;-2\right)\).
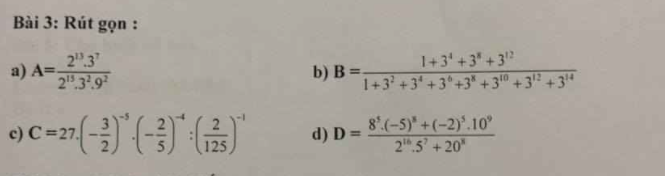 giúp mình với ạ cả 4 câu càng nhanh càng tốt
giúp mình với ạ cả 4 câu càng nhanh càng tốt
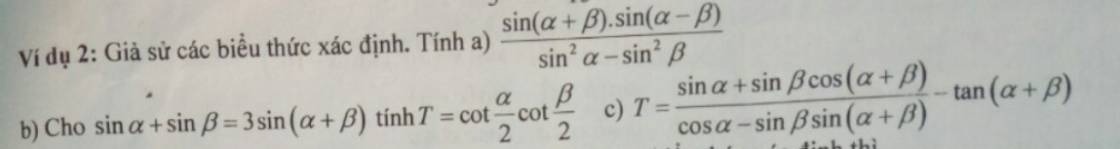
 giúp mình với ạ càng nhanh càng tốt 4 câu trên ạ
giúp mình với ạ càng nhanh càng tốt 4 câu trên ạ






2: FK vuôg góc BE; AE vuông góc BE
=>FK//AE
Chứng minh tương tự, ta được AF//EK
=>AFKE là hbh
=>AF=EK
=>AF/EC=EK/EC
ΔCEK đồng dạng với ΔCAM
=>EK/EC=AM/AC
=>AF/EC=AM/AC
ΔAFB đồng dạng với ΔCEB
=>góc ABF=góc CBE
c: AM/AC=AF/EC=AB/BC
=>AM/AC=AB/BC
=>ΔAMB đồng dạng với ΔCAB
=>góc ABC=góc ABM
=>BA là phân giác của góc MBC