Cho hình thang ABCD(AB//CD). Gọi Ơ là giao điểm hai đường chéo, Sabc=a, Scdo= b. a. Chứng minh Saod= Sbco b. Tính Saod
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
4 tháng 5 2022
a/
Hai tg ABD và tg ABC có chung AB và đường cao từ D->AB = đường cao từ C->AB nên \(S_{ABD}=S_{ABC}\)
Hai tg này có phần diện tích chung là \(S_{ABO}\Rightarrow S_{AOD}=S_{BOC}\)
b/
Hai tg ABC và tg ACD có đg cao từ D->AB = đường cao từ B->CD nên
\(\dfrac{S_{ABC}}{S_{ACD}}=\dfrac{AB}{CD}=\dfrac{1}{2}\)
Hai tg trên có chung AC nên
\(\dfrac{S_{ABC}}{S_{ACD}}=\) đg cao từ B->AC / đg cao từ D->AC\(=\dfrac{1}{2}\)
Hai tg ABO và tg AOD có chung AO nên
\(\dfrac{S_{ABO}}{S_{AOD}}=\) đg cao từ B->AC / đg cao từ D->AC\(=\dfrac{1}{2}\)
\(\Rightarrow S_{AOD}=2xS_{ABO}=2x3,5=7cm^2\)
\(\Rightarrow S_{ABD}=S_{ABO}+S_{AOD}=3,5+7=10,5cm^2\)
Hai tg ABD và tg BCD có đg cao từ D->AB = đường cao từ B->CD nên
\(\dfrac{S_{ABD}}{S_{BCD}}=\dfrac{AB}{CD}=\dfrac{1}{2}\Rightarrow S_{BCD}=2xS_{ABD}=2x10,5=21cm^2\)
\(\Rightarrow S_{ABCD}=S_{ABD}+S_{BCD}=10,5+21=31,5cm^2\)
PT
0
28 tháng 6 2023
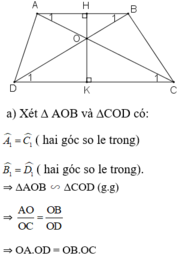
a: Xét ΔFAB và ΔFCD có
góc FAB=góc FCD
góc AFB=góc CFD
=>ΔFAB đồng dạng với ΔFCD
b: ΔFAB đồng dạng với ΔFCD
=>FA/FC=FB/FD
=>FA*FD=FB*FC
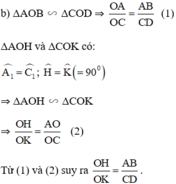
Ta thấy tam giác ACD và tam giác BCD có chung đáy cd , chiều cao bằng nhau và bằng chiều cao hình thang ABCD . Nên Sacd=Sbcd. Suy ra Saod=Sboc
b) cho diện tích abo=a thì chắc mình mới làm được nhé....
Xét tam giác aob và cod có
aob=cod (đối đỉnh), abo=cdo(so le trong do ab//cd)
Suy ra 2 tam giác này đồng dạng
=> (Ao/oc)^2=Saob/Scod=a/b
Xét tam giác aod và cdo chung đường cao hạ từ d xuống ac. Suy ra Saod/Scod=ao/co= căn (a/b)
=> Saod= căn (a/b) * b= căn (ab)
Kết quả đúng ạ mà mik có cách ngắn hơn rồi, cảm ơn bạn đã giúp ạ😄