Một vật sáng AB=2cm đặt vuông góc với trục chính của một tkht tiêu cự f=12cm, ảnh thật A'B'=4cm. Khoảng cách từ vật đến thấu kính là bao nhiêu ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


b)Ảnh thật.
c)Để ảnh thật cao gấp đôi vật \(\Rightarrow h'=2h\) thì:
\(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow\dfrac{h}{2h}=\dfrac{d}{d'}=\dfrac{1}{2}\Rightarrow d'=2d\)
Khi đó vị trí cách thấu kính là:
\(d'=2d=2\cdot50=100cm\)

Đáp án: C
HD Giải:
Khi dời vật lại gần ![]() thì ảnh dời ra xa
thì ảnh dời ra xa ![]()
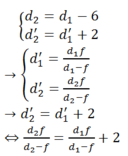
Mà d2 = d1 – 6
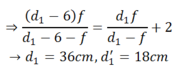

a) Ảnh thật vì d > f
b) 
\(\Delta ABF\sim\Delta OIF\)
\(\Rightarrow\dfrac{AB}{OI}=\dfrac{AF}{OF}\Leftrightarrow\dfrac{AB}{A'B'}=\dfrac{OA-OF}{OF}\Leftrightarrow\dfrac{2}{A'B'}=\dfrac{15-10}{10}\)
=> A'B' = 4cm
\(\Delta ABO\sim\Delta A'B'O\)
\(\Rightarrow\dfrac{AB}{A'B'}=\dfrac{OA}{OA'}\Rightarrow OA'=\dfrac{OA.A'B'}{AB}=\dfrac{15.4}{2}=30cm\)

Ta có:
\(\dfrac{1}{d}+\dfrac{1}{d'}=\dfrac{1}{f}\)
\(\Rightarrow\dfrac{1}{16}+\dfrac{1}{d'}=\dfrac{1}{12}\)
\(\Rightarrow d'=48\)
Vậy khoảng cách từ ảnh đến thấu kính là 48cm
\(k=\dfrac{d'}{d}=\dfrac{A'B'}{AB}=2\Rightarrow d'=2d\)
\(\dfrac{1}{d'}+\dfrac{1}{d}=\dfrac{1}{f}\Leftrightarrow\dfrac{1}{2d}+\dfrac{1}{d}=\dfrac{1}{12}\Rightarrow d=18\left(cm\right)\)