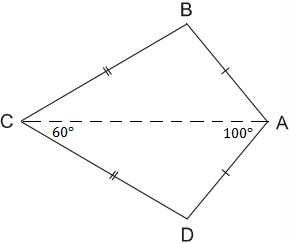
Ta gọi tứ giác ABCD trên hình 8 có AB= AD=CD là hình cái diều
a chứng minh rằng ac là đg trung trực của BD
b tính Góc b. góc d biết rằng góc a=100..góc c =60 ở SGK lớp 8 trang 67 bài 3 nhé ai giải hộ với
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: AB = AD (gt) => A thuộc đường trung trực của BD
CB = CD (gt) => C thuộc đường trung trực của BD.
Vậy AC là đường trung trực của BD.
b) Xét ∆ ABC và ∆ADC có AB = AD (gt)
nên ∆ ABC = ∆ADC (c.c.c)
Suy ra: ⇒ˆB=ˆD
Ta có ˆB+ˆD=3600–(100+60)=200
Do đó ˆB=ˆD=1000

a) ta thấy ab = ab ; bc = cd
=> tứ giác ABCD là hình bình hành
=> AC và BD cắt nhau tai trung điểm của mỗi đường
=> AC là đường trung trực của BD
b) Ta có A + D = 180
=> D = 180 - 100
=> D= 80
Ta lại có B + C = 180
=> C = 180 - 60
=> C = 120

a) Ta có:
AB = AD (gt) ⇒ A thuộc đường trung trực của BD
CB = CD (gt) ⇒ C thuộc đường trung trực của BD
Vậy AC là đường trung trực của BD
b) Xét ΔABC và ΔADC có:
AB = AD (gt)
BC = DC (gt)
AC cạnh chung
⇒ ΔABC = ΔADC (c.c.c)
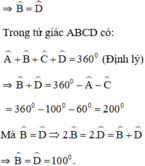

a) Ta có: AB = AD (gt) => A thuộc đường trung trực của BD
CB = CD (gt) => C thuộc đường trung trực của BD.
Vậy AC là đường trung trực của BD.
b) Xét ∆ ABC và ∆ADC có AB = AD (gt)
BC = DC (gt)
AC cạnh chung
nên ∆ ABC = ∆ADC (c.c.c)

Suy ra: ⇒ \(\widehat{B}=\widehat{D}\)
Ta có \(\widehat{B}+\widehat{D}=360^o-\left(100^o+60^o\right)=200^o\)
Do đó \(\widehat{B}=\widehat{D}=100^o\)
Bài giải:
a) Ta có: AB = AD (gt) => A thuộc đường trung trực của BD
CB = CD (gt) => C thuộc đường trung trực của BD.
Vậy AC là đường trung trực của BD.
b) Xét ∆ ABC và ∆ADC có AB = AD (gt)
BC = DC (gt)
AC cạnh chung
nên ∆ ABC = ∆ADC (c.c.c)

Suy ra:
Ta có
Do đó

a) Ta có:
\(AB = AD\) (gt) nên \(A\) thuộc đường trung trực của \(BD\)
\(CB = CD\) (gt) nên \(C\) thuộc đường trung trực của \(BD\)
Vậy \(AC\) là đường trung trực của \(BD\)
b) Xét \(\Delta ABC\) và \(\Delta ADC\) ta có:
\(AB = AD\) (gt)
\(BC = CD\) (gt)
\(AC\) chung
Suy ra: \(\Delta ABC = \Delta ADC\) (c-g-c)
Suy ra: \(\widehat {ABC} = \widehat {ADC} = 95^\circ \) (hai góc tương ứng)
Trong tứ giác \(ABCD\), tổng các góc bằng \(360^\circ \) nên:
\(\widehat A = 360^\circ - \left( {95^\circ + 35^\circ + 95^\circ } \right) = 135^\circ \)