Rút gọn biểu thức P=A+B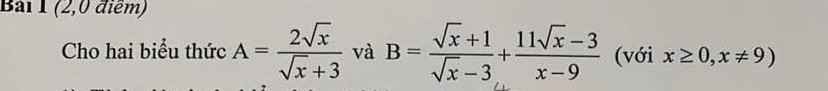
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
6 tháng 7 2018
a) Thay phân thức P vào biểu thức A rồi rút gọn chúng ta thu được A = u + v với điều kiện các biểu thức có nghĩa.
b) Tương tự a) ta có B = 1.
U
1
KK
24 tháng 2 2019
A = -{-(a + b) - [-(a - b) - (a + b)]}
= -{-a - b - [-a + b - a - b]}
= -[-a - b - (-2a)]
= -(-a - b + 2a)
= -(a - b)
= -a + b
TT
5
CM
20 tháng 5 2019
a) a ≠ 0 , a ≠ − 5
b) Ta có A = a 3 + 4 a 2 − 5 a 2 a ( a + 5 ) = a ( a − 1 ) ( a + 5 ) 2 a ( a + 5 ) = a − 1 2
c) Thay a = -1 (TMĐK) vào a ta được A = -1
d) Ta có A = 0 Û a = 1 (TMĐK)
HT
2
MH
29 tháng 1 2016
A = (-a + b - c) - (-a - b - c)
= -a + b - c + a + b + c
= (a - a) + (b + b) + (c - c)
= 0 + 2b + 0
= 2b
29 tháng 1 2016
A = ( -a + b - c) - (-a - b - c)
= -a + b - c + a + b + c
= 2b
DD
2
YS
3 tháng 5 2016
Cho biểu thức: A = (-a + b - c) - (-a - b - c)
Rút gọn biểu thức A
Giải:
A = (-a + b - c) - (-a - b - c)
Chuyển hai vế ta được:
A = (-a + a) + (b + b) + (-c + c)
A = 0 + 2b + 0
A = 2b
\(B=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}+\dfrac{11\sqrt{x}-3}{x-9}\)
\(B=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}+\dfrac{11\sqrt{x}-3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(B=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}+3\right)+11\sqrt{x}-3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(B=\dfrac{x+3\sqrt{x}+\sqrt{x}+3+11\sqrt{x}-3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(B=\dfrac{x+15\sqrt{x}}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(P=A+B=\dfrac{2\sqrt{x}}{\sqrt{x}+3}+\dfrac{x+15\sqrt{x}}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(P=\dfrac{2\sqrt{x}\left(\sqrt{x}-3\right)+x+15\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(P=\dfrac{2x-6\sqrt{x}+x+15\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(P=\dfrac{3x+9\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(P=\dfrac{3\sqrt{x}\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(P=\dfrac{3\sqrt{x}}{\sqrt{x}-3}\)