Một thỏi thép nặng 12kg đang có nhiệt độ 15oC biết C của thép bằng 460J/kg.K nếu khối thép này nhận thêm một nhiệt lượng 44160J thì nhiệt lượng của nó tăng lên bao nhiêu?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
H9
HT.Phong (9A5)
CTVHS
24 tháng 4 2023
Tóm tắt:
\(m=12kg\)
\(t_1=20^oC\)
\(c=460J/kg.K\)
\(Q=44160J\)
============
\(\Delta t=?^oC\)
Nhiệt độ mà miếng thép tăng lên:
\(Q=m.c.\Delta t\Rightarrow\Delta t=\dfrac{Q}{m.c}=\dfrac{44160}{12.460}=8^oC\)
Vậy nhiệt độ của thỏi thép khi tăng lên:
\(\Delta t=t_2-t_1\Rightarrow t_2=\Delta t+t_1=8+20=28^oC\)
DT
Đỗ Thanh Hải
CTVVIP
1 tháng 5 2021
Qthu = Qtoả
2.4200.(x-40) = 0,3.460(80-x)
=> 8400x-336000 = 11040 - 138x
=> 8538x = 347040
=> x = 40,65
Vậy nước sẽ nóng thêm: 40,65 - 40 = 0,65 độ
1 tháng 5 2021
\(m_1=0,3kg\\ t_1=80^oC\\ m_2=2kg\\ t_2=40^oC\\ c_2=4200J/kg.K\\ c_1=460J/kg.K\\ \Delta t_2=?\)
GIẢI
Nhiệt lượng quả cầu tỏa ra là:
\(Q_1=m_1.c_1.\left(t_1-t\right)=0,3.460.\left(80-t\right)\left(J\right)\)
Nhiệt lượng nước thu vào là:
\(Q_2=m_2.c_2.\left(t-t_2\right)=2.4200.\left(t-40\right)\left(J\right)\)
Theo phương trình cân bằng nhiệt:
\(Q_{tỏa}=Q_{thu}\\ \Rightarrow Q_1=Q_2\\ \Rightarrow0,3.460.\left(80-t\right)=2.4200.\left(t-40\right)\\ \Rightarrow11040-138t=8400t-336000\\ \Rightarrow8400t+138t=11040+336000\\ \Rightarrow8538t=347040\\ \Rightarrow t=\dfrac{347040}{8538}\approx40,65\left(^oC\right)\\ \Rightarrow\Delta t_2=40,65-40=0,65\left(^oC\right)\)
Vậy nước nóng thêm 0,65oC khi có cân bằng nhiệt.
Y
9 tháng 5 2023
\(m=5kg\)
\(t_1=25^oC;t_2=26^oC\)
\(\Rightarrow\Delta t=t_2-t_1=26-25=1^oC\)
\(c=460J/kg.K\)
\(Q=?J\)
======================
Nhiệt lượng cần truyền là :
\(Q=m.c.\Delta t=5.460.1=2300\left(J\right)\)
9 tháng 5 2023
Nhiệt lượng cần truyền cho thép :
\(Q=c.m.\Delta t=460.5.1=2300\left(J\right)\)
NV
12 tháng 5 2023
Tóm tắt:
t1 = 345oC
c1 = 460J/KgK
m2 = 3kg
t2 = 25oC
c2 = 4200J/KgK
to = 33oC
m1 = ?
------------------------------------
Nhiệt lượng thu vào của nước là:
Qthu = \(m_1\cdot c_1\cdot\left(t^o-t_2\right)\)
= \(3\cdot4200\cdot\left(33-25\right)\)
= 100800 (J)
Theo phương trình cân bằng nhiệt:
Qthu = Qtỏa = 100800J
Qtỏa = \(m_1\cdot c_1\cdot\left(t_1-t^o\right)\)
100800J = \(m_1\cdot460\cdot\left(345-33\right)\)
=> m1 = \(\dfrac{100800}{460\cdot\left(345-33\right)}\) = 0,7 (kg)
TC
29 tháng 3 2023
a) khối thép thu nhiệt do tăng nhiệt độ
b) Nhiệt lương cần truyền cho khối thép
`Q = mc*(t_2-t_1) = 2*460*(250-20)=211600(J)`
9 tháng 5 2021
Tóm tắt
\(t_1=260^0C\)
\(c_1=\) 460 J/Kg.K
\(t_2=20^0C\)
\(c_2=\) 4200 J/Kg.K
\(m_2=2kg\)
\(t=50^0C\)
a) \(Q=?J\) ; b) \(m_1=?kg\)
Giải
Nhiệt lượng thu vào của nước là:
\(Q_2=m_2\cdot c_2\cdot\left(t-t_2\right)=2\cdot4200\cdot\left(50-20\right)=252000\left(J\right)\)
Nhiệt lượng của quả cầu bằng nhiệt lượng của nước thu vào
\(Q_1=Q_2=252000\left(J\right)\)
Khối lượng của quả cầu là
\(Q_1=m_1\cdot c_1\cdot\left(t_1-t\right)\)
\(\Rightarrow m_1=\dfrac{Q_1}{c_1\cdot\left(t_1-t\right)}\)
\(\Rightarrow m_1=\dfrac{252000}{460\cdot\left(260-50\right)}=2,6\left(kg\right)\)
DD
2 tháng 5 2019
a, Nhiệt lượng thép tỏa ra là :
Q2 = m2 . c2 . ( t1 - t ) = 0,6 . 460 . ( 120 - 40 ) = 22080 (J )
Vậy nhiệt lượng thép tỏa ra là 22080J
b, Theo phương trình cân bằng nhiệt, ta có :
Q1 = Q2 => 3 . 4200 . ( t2 - t1 ) = 22080
<=> t2 - t1 ~ 1,75
=> t2 ~ 1,75 + 40 = 41,75
Vậy nhiệt độ ban đầu của nước là 41,75.
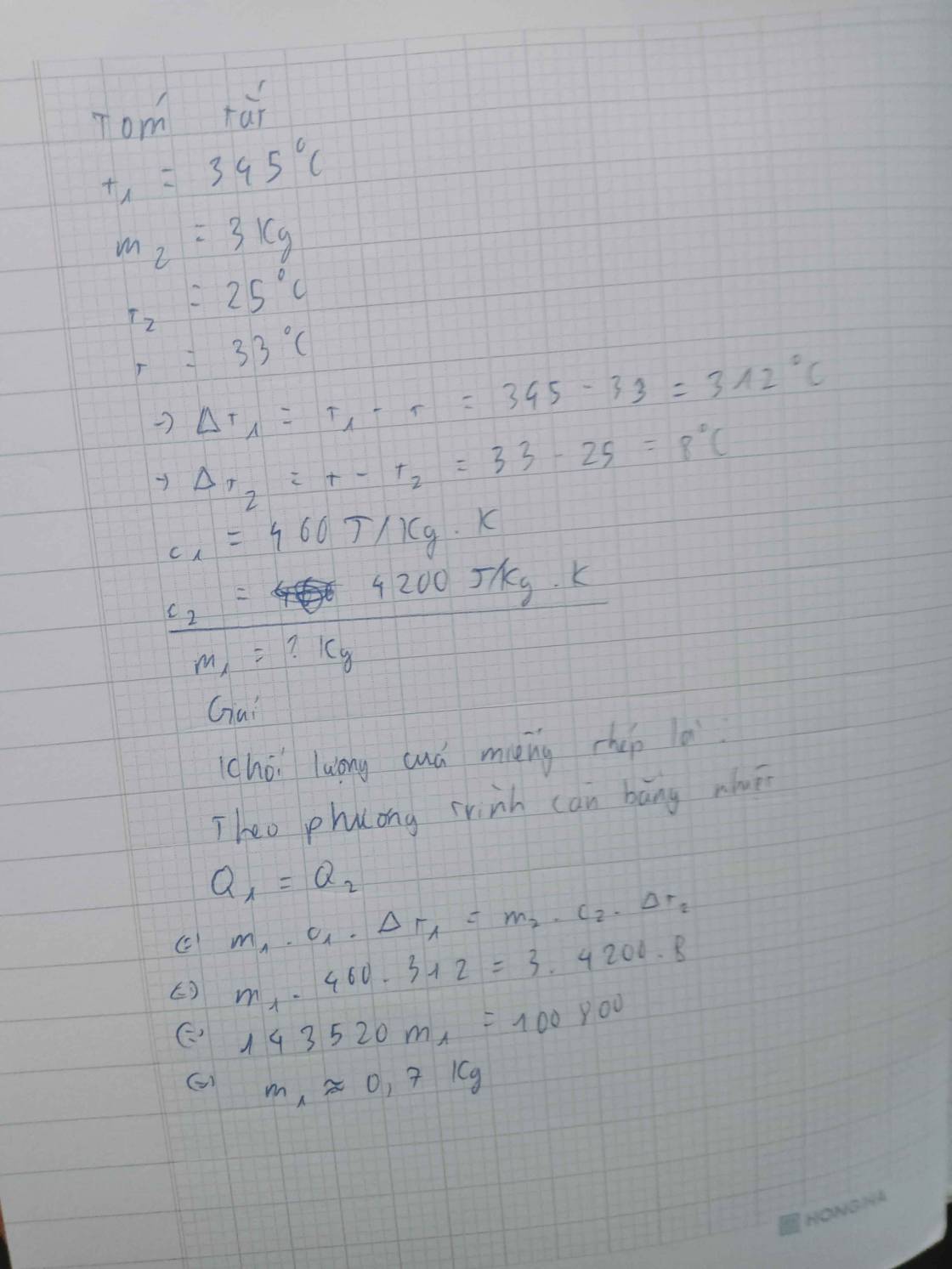
Tóm tắt:
m = 12 kg
C = 460 J/kg.K
t0 = 20oC
Q = 44160J
t = ?
Giải:
Nhiệt độ của thỏi thép sau khi nhận nhiệt lượng:
Q = m.c(t − t0)
→ t = t0 + Q/mc = 15 + 44160/12.460 = 28oC
Ơ cái này phải là nhiệt độ của nó tăng lên bao nhiêu mà :))??
Nhiệt độ của thỏi thép là
\(Q=mc\Delta t\\ =12.460\left(t-15\right)=44160\\ \Rightarrow t=23^o\)