Tam giác ABC có góc A = 60o. Các tia phân giác góc B, C cắt nhau tại I & cắt cạnh AC tại D, AB tại E. CMR: Tam giác IDE cân tại I
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


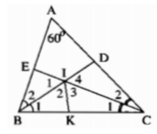
Trong ΔABC, ta có:
∠A +∠B +∠C = 180o (tổng ba góc trong tam giác)
⇒∠B +∠C = 180 - ∠A = 180 - 60 = 120o
+) Vì BD là tia phân giác của ABC nên: ∠(B1 ) = ∠(B2) = 1/2 ∠B
Vì CE là tia phân giác của góc ACB nên: ∠(C1 ) = ∠(C2) = 1/2 ∠ C
Do đó:
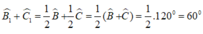
Trong ΔBIC, ta có:
∠(BIC) = 180o(∠(B1 ) + ∠(C1) = 180o - 60o = 120o
Kẻ tia phân giác ∠(BIC) cắt cạnh BC tại K
Suy ra: ∠(I2 ) = ∠(I3 ) = 1/2 ∠(BIC) = 60o
Ta có: ∠(I1 ) + ∠(BIC) = 180o (hai góc kề bù)
⇒ ∠(I1 ) = 180o-∠(BIC) = 180o - 120o = 60o
∠(I4 ) = ∠(I1) = 60o(vì hai góc đối đỉnh)
Xét ΔBIE và ΔBIK, ta có
∠(B2) = ∠(B1) (vì BD là tia phân giác của góc ABC)
BI cạnhchung
∠(I1) = ∠(I2) = 60o
Suy ra: ΔBIE = ΔBIK(g.c.g)
IK = IE (hai cạnh tương ứng) (1)
Xét ΔCIK và ΔCID, ta có
∠(C1) = ∠(C2) ( vì CE là tia phân giác của góc ACB).
CI cạnh chung
∠(I3) = ∠(I4) = 60o
Suy ra: ΔCIK = ΔCID(g.c.g)
IK = ID (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra: IE = ID

Trong tam giác ABC có góc BAC + ABC + ACB = 180 độ
\(\Rightarrow\) góc ABC + góc ACB = 180 độ - góc BAC = 180 độ - 60 độ = 120 (độ)
Ta có góc IBC + góc ICB = góc ABC/2 + góc ACB/2 = (góc ABC + góc ACB)/2 = 120 độ/2 = 60 (độ)
Trong tam giác IBC có góc BIC + góc IBC + góc ICB = 180 độ
\(\Rightarrow\) góc BIC = 180 độ - (góc IBC + góc ICB) = 180 độ - 60 độ = 120 độ

Bạn xem ở đường link này:
Câu hỏi của Cùng học toán đi - Toán lớp 6 - Học toán với OnlineMath

Hình vẽ a chèn không rõ được không, chắc giống của e thôi.
https://1drv.ms/u/s!AhUPZHs4UJtKilHrVZWqF8i6a584?e=0TIfMP
Ta có : \(\widehat{BIC}=180^0-\widehat{IBC}-\widehat{ICB}\)( Do tổng ba góc trong một tam giác bằng 180 độ)
\(\Rightarrow\widehat{BIC}=180^0-\frac{\widehat{ABC}}{2}-\frac{\widehat{ACB}}{2}\)( Do IB,IC là tia phân giác của góc ABC và ACB)
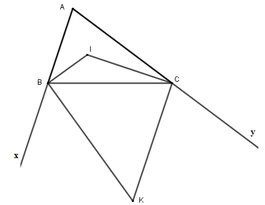
còn \(\widehat{BKC}=180^0-\widehat{KBC}-\widehat{KCB}\)( Do tổng ba góc trong một tam giác bằng 180 độ)
\(\Rightarrow\widehat{BKC}=180^0-\frac{\widehat{xBC}}{2}-\frac{\widehat{yCB}}{2}\)( Do KB,KC là tia phân giác của góc ABC và ACB)
Mà \(\hept{\begin{cases}\widehat{xBC}=180^0-\widehat{ABC}\\\widehat{yCB}=180^0-\widehat{ACB}\end{cases}}\)\(\Rightarrow\widehat{BKC}=180^0-\left(\frac{180^0-\widehat{ABC}}{2}+\frac{180^0-\widehat{ACB}}{2}\right)\)
\(\Rightarrow\widehat{BKC}=\frac{\widehat{ABC}}{2}+\frac{\widehat{ACB}}{2}\)



Kẻ IH là tia phân giác BIC
Ta có góc CBD=ABD=1/2*B ( BD là tia phân giác góc B)
Góc BCE=ACE=1/2*C (CE là tia phân giác C)
Mà góc A+B+C=180 độ (định lí)
=> Góc B+C=180-A=180-60=120 độ
=> Góc CBD+BCE=1/2(B+C)=1/2*120=60
Trong tam giác BIC có góc BIC=180-(CBD+BCE)=180-60=120 độ
=> góc BIH=CIH=1/2*BIC=60( IH là tia phân giác)
góc BIF=180-BIC (kề bù)=180-120=60
Và CID=BIE=60 độ (đối đỉnh)
Xét tam giác BIE và tam giác BIH có:
BIE=BIH(cmt)
BI là cạnh chung
CBD=ABD(phân giác BD)
=> Tam giác BIE=tam giác BIH(g-c-g)
=> IE=IH( 2 cạnh tương ứng)
Xét tam giác CIH và tam giác CID có:
IC chung
CID=CIH(cmt)
BCE=ECA( phân giác CE)
=> Tam giác CIH=tam giác CID(g-c-g)
=> IH=ID( 2 cạnh tương ứng)
Do IH=ID và IE=IH
=> IH=ID=IE
=> ID=IE
Tam giác ABC ( góc A=60 độ)
BD là tia phân giác góc B
CE là tia phân giác góc C
BD∩CE={I}