so sánh 202303 và 303202
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
19 tháng 7 2023
`@` `\text {Ans}`
`\downarrow`
\(202^{303}\text{ và }303^{202}\)
Ta có:
\(202^{303}=202^{3\cdot101}=\left(202^3\right)^{101}\)
\(303^{202}=303^{101\cdot2}=\left(303^2\right)^{101}\)
So sánh `202^3` và `303^2`, ta có:
`202^3 = (2*101)^3 = 2^3 * 101^3 = 8 * 101^3 = 8* 101^2 * 101 = 808*101^2`
`303^2 = (3*101)^2 = 3^2 * 101^2 = 9 * 101^2`
Vì `9 < 808 \Rightarrow 9*101^2 < 808*101^2`
`\Rightarrow`\(202^{303}>303^{202}\)
Vậy, \(202^{303}>303^{202}.\)
25 tháng 3 2016
202^303 = 202^3x101= (202^3)^101=8242408^101
303^202 = 303^2x101= (303^2)^101=91809^101
vì 8242408^101> 91809^101
=> 202^303 > 303^202
vậy .. .
ủng hộ nhé
28 tháng 11 2015
Ta co : 202303 va 303202
=> 202303=(2022)101=40804101 (1)
=>303202=(3033)101=27818127101 (2)
Tu (1) va (2) suy ra 202303<303202
lik e nhe
LV
24 tháng 9 2017
202303=2023x101=(2023)101=8242408101
303202=3032x101=(3032)101=91809101
Vì 8242408101 > 91809101
=> 202303 > 91809101
24 tháng 9 2017
Ta có:
\(202^{303}=\left(101.2\right)^{303}=101^{606}\)
\(303^{202}=\left(101.3\right)^{202}=101^{606}\)
Vì \(101^{606}=101^{606}\)nên \(202^{303}=303^{202}\)
Vậy \(202^{303}=303^{202}\)
30 tháng 9 2015
Ta có : 303^202 = ( 303^2)^101 = 91809^101
202^303 = ( 202^3)^101 = 8242408^101
Vì 8242408^101 > 91809^101
Nên 303^202 < 202^303
30 tháng 9 2015
Ta có :
303202 = 101202 . 3202 = 101202 . (32)101 = 101202 . 9101
202303 = 101303 . 2303 = 101303 . (23)101 = 101303 . 8101
Vì 101202 < 101303 ; 9101 > 8101
=> không so sánh được
HT
15 tháng 10 2019
\(202^{303}=\left(202^3\right)^{101}=\text{8,242,408}^{101}\)
\(303^{202}=\left(303^2\right)^{101}=\text{91,809}^{101}\)
Vì : \(\text{8,242,408}^{101}>91809^{101}\)
Nên :\(202^{303}>303^{202}\)
SM
20 tháng 9 2018
202303 = ( 2023 )101 = 8242408101
303202 = ( 3032 )101 = 91809101
Vì 8242408 > 91809
=> 8242408101 > 91809101
=> 202303 > 303202
20 tháng 9 2018
202303 = ( 2023 )101 = 8242408101
303202 = ( 3032 )101 = 91809101
Vì 8242408 > 91809
=> 8242408101 > 91809101
=> 202303 > 303202
12 tháng 8 2016
202303=(2023)101
303202=(3032)101
ta có:
2023=23.1013=8.1013=808.1012
3032=32.1012=9.1012=9.1012
vì 808>9
=> 2023>3032
=> 202303>303202
12 tháng 8 2016
\(202^{203}=\left(2.101\right)^{3.101}=\left(1^3.101^3\right)^{101}=\left(8.101.10^{12}\right)^{101}=\left(808.1012\right)^{101}\)
\(303^{202}=\left(3.101\right)^{2.101}=\left(32.101^2\right)^{101}=\left(9.101^2\right)^{101}\)
\(\Rightarrow\left(80^{ }8.101^2\right)>\left(9.101^2\right)\)
Vậy:
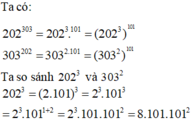
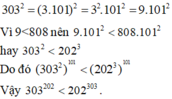
202303 = ( 2.101 )3.101 = ( 23.1013)101 = (8.1013)101
303202 = (3.101)2.101 = (32.1012)101 = (9.1012)101
Ta có : 8.1013 = 8.101.1012 > 9.1012
=> 202303 > 303202