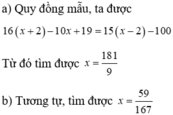Giải phương trình : √2x+15=32x2+32x−202x+15=32x2+32x−20
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 6 2019
a,
ĐK : \(x\ge\frac{-15}{2}\)
Phương trình đã cho tương đương với
\(\sqrt{2x+15}=32x^2+32x-20\)
\(\Leftrightarrow2x+15=\left(32x^2+32x-20\right)^2\)\(\Leftrightarrow1024x^4+2048x^3-256x^2-1282x+385=0\)
Phương trình này có 2 nghiệm là \(\orbr{\begin{cases}x=\frac{1}{2}\\x=\frac{-11}{8}\end{cases}}\) nên dễ dàng có được
⇔ ( 16x2 + 14x − 11 ) ( 64x2 + 72x − 35 ) = 0
Kết hợp với điều kiên bài toán ta có nghiệm của phương trình là \(x=\frac{1}{2};x=\frac{-9-\sqrt{221}}{16}\)
15 tháng 6 2019
b,\(x^2=\sqrt{2-x}+2\)
ĐK \(x\le2\)
\(PT\Leftrightarrow\sqrt{2-x}=x^2-2\)
\(\Leftrightarrow2-x=\left(x^2-2\right)^2=x^4-4x^2+4\)
\(\Leftrightarrow x^4-4x^2+x+2=0\Leftrightarrow\left(x-1\right)\left(x^3+x^2-3x-2\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+2\right)\left(x^2-x-1\right)=0\)
Vì\(x^2-x-1>0\)nên
\(\orbr{\begin{cases}x-1=0\\x+2=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=1\\x=-2\end{cases}\left(Tm\right)}}\)
26 tháng 11 2018
\(\sqrt{2x+15}=32x^2+32x-20\)(1)
ĐK : \(x\ge-\dfrac{15}{2}\)
\(\left(1\right)\Leftrightarrow\sqrt{2x+15}-4=32x^2+32x-24\)
\(\Leftrightarrow\dfrac{2x-1}{\sqrt{2x+15}+4}=\left(2x-1\right)\left(2x+3\right)\)
\(\Leftrightarrow\left(2x-1\right)\left(\dfrac{1}{\sqrt{2x+15}+4}-\left(2x+3\right)\right)=0\)
Làm tiếp nhé!!
PT
1
CM
9 tháng 4 2018
Hướng dẫn:
Ta có:
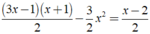
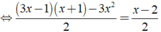
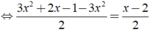
⇔ 2x - 1 = x - 2 ⇔ x = - 1.
Vậy phương trình đã cho có tập nghiệm là S = { - 1 }.
PT
1
CM
31 tháng 1 2017
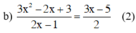
Điều kiện xác định: 2x – 1 ≠ 0 ⇔ x ≠ 1/2.
Quy đồng và bỏ mẫu chung ta được:
Phương trình (2) ⇔ 2(3x2 – 2x + 3) = (2x – 1)(3x – 5)
⇔ 6x2 – 4x + 6 = 6x2 – 10x – 3x + 5
⇔ 9x = –1
⇔ x = –1/9 (thỏa mãn đkxđ)
Vậy phương trình có nghiệm là x = –1/9.