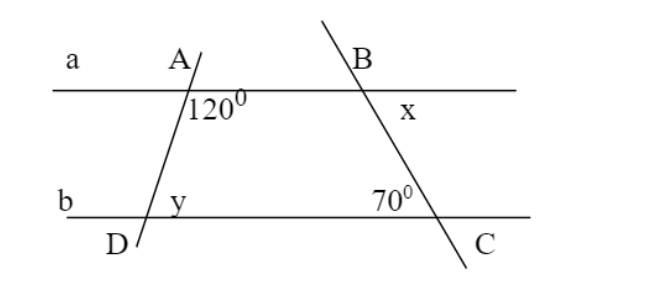
Tìm $x,$ $y$ trong hình vẽ sau:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a) 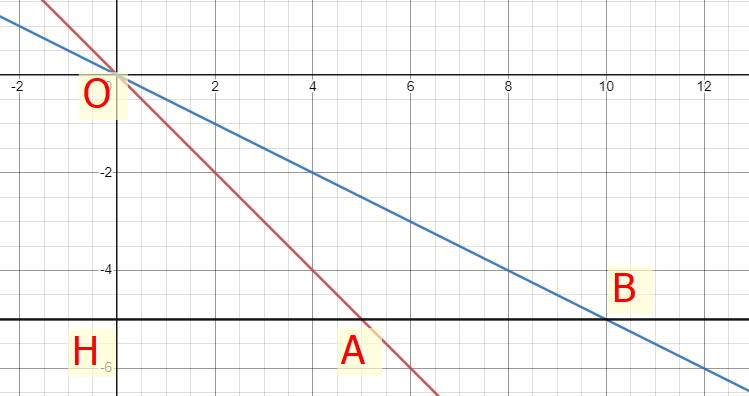
b) Ta có đường thẳng đi qua điểm H(0;-5) nên phương trình đường thẳng đi qua H là:
\(y=0x-5\Rightarrow y=-5\)
Phương trình hoành độ giao điểm của đường thẳng \(y=-5\) và \(y=-x\) là:
\(-5=-x\)
\(\Rightarrow x=5\)
Tọa độ điểm A là (5;-5)
Phương trình hoành độ giao điểm của đường thẳng \(y=-5\) và \(y=-\dfrac{1}{2}x\) là:
\(-5=-\dfrac{1}{2}x\)
\(\Rightarrow\dfrac{1}{2}x=5\)
\(\Rightarrow x=5:\dfrac{1}{2}\)
\(\Rightarrow x=10\)
Tọa độ điểm B là (10;-5)
c) Ta có: A(5;-5) và B(10;-5)
Độ dài đường thẳng AB là \(10-5=5\left(đvđd\right)\)
Có A(5;-5) ⇒ HA = 5 (đvđd)
Xét tam giác OHA vuông tại H áp dụng định lý Py-ta-go ta có:
\(OA^2=HA^2+OH^2\) (tọa độ điểm H(0;-5) nên OH = 5 đvđd)
\(\Rightarrow OA=\sqrt{5^2+5^2}=\sqrt{50}=5\sqrt{2}\left(đvđd\right)\)
Có B(10;-5) ⇒ HB = 10 (đvđd)
Xét tam giác OHB vuông tại H áp dụng định lý Py-ta-go ta có:
\(OB^2=HB^2+OH^2\)
\(\Rightarrow OB=\sqrt{10^2+5^2}=\sqrt{125}=5\sqrt{5}\left(đvđd\right)\)
Chu vi: \(C_{OAB}=AB+OA+OB=5+5\sqrt{2}+5\sqrt{5}\approx23,25\left(đvđd\right)\)
Diện tích: \(S_{OAB}=\dfrac{1}{2}\cdot OH\cdot AB=\dfrac{1}{2}\cdot5\cdot5=12,5\left(đvdt\right)\)

vì a//b nên A+y=180(trong cùng phía
=>y=180-A=180-120=60
vì a//b nên x=C=70(so le trong)

Lời giải:
Hàm số chẵn là hàm số được xác định như sau:
Với mọi $x\in D thì -x\in D$ và $f(x)=f(-x)$
Dựa vào định nghĩa này ta có thể thấy:
Với $x\in\mathbb{R}\Rightarrow -x\in\mathbb{R}$:
\(y(x)=|x^2-1|+x\)
\(y(-x)=|(-x)^2-1|+(-x)=|x^2-1|-x\)
Ta thấy việc $y(x)=y(-x)$ không xảy ra với mọi $x,-x\in\mathbb{R}$
Do đó hàm số ở phần $D$ không phải hàm chẵn

a: Khi y=-5 thì 1/2x=-5
hay x=-10
Khi y=10 thì 1/2x=10
hay x=20
Khi y=13 thì 1/2x=13
hay x=26
c: Khi x=5/2 thì \(y=\dfrac{1}{2}\cdot\dfrac{5}{2}=\dfrac{5}{4}< >0\)
=>A không thuộc đồ thị
Khi x=1 thì \(y=\dfrac{1}{2}\cdot1=\dfrac{1}{2}< >6\)
=>B không thuộc đồ thị
Khi x=-3/2 thì \(y=\dfrac{1}{2}\cdot\dfrac{-3}{2}=\dfrac{-3}{4}< >-4\)
=>C không thuộc đồ thị
Khi x=-1/2 thì \(y=\dfrac{1}{2}\cdot\dfrac{-1}{2}=\dfrac{-1}{4}< >-6\)
=>D không thuộc đồ thị




tam giác ABC vuông tại A có AT là đường cao
Áp dụng định lí Py ta go ta có : \(AB^2+AC^2=BC^2\Rightarrow25-AB^2=AC^2\)(1)
* Theo hệ thức : \(\frac{1}{AB^2}+\frac{1}{AC^2}=\frac{1}{AT^2}\Rightarrow\frac{1}{4}=\frac{1}{AB^2}+\frac{1}{25-AB^2}\)( theo 1 )
\(\Rightarrow AB=2\sqrt{5};\sqrt{5}\)
TH1 : \(25-\left(2\sqrt{5}\right)^2=AC\Rightarrow AC=\sqrt{5}\)
TH2 : \(25-\left(\sqrt{5}\right)^2=AC\Rightarrow AC=2\sqrt{5}\)
Gọi BH là z ( z>0), thì HC là 5-z
ΔABC vuông tại A có:
AH.BC=BH.HC (định lý 3)
⇔ 22 = z(5-z)
⇔ z2 - 5z + 4 = 0
⇔ z(z-1) - 4(z-1) = 0
⇔(z-4)(z-1)=0
⇔\(\left[{}\begin{matrix}z-4=0\\z-1=0\end{matrix}\right.\)
⇔\(\left[{}\begin{matrix}z=4\left(nhận\right)\\z=1\left(nhận\right)\end{matrix}\right.\)
TH1:Nếu z=4
ΔABC vuông tại A có:
x2=BC.BH ( định lý 1)
⇔ x2= 5.4
⇔ x2= 20
⇒x=\(2\sqrt{5}\)
ta có: y2= BC.HC ( định lý 1)
Chứng minh tương tự như trên ta được
y= \(\sqrt{5}\)
TH2: Nếu z=1
Chứng minh tương tự như TH1 ta được:
x=\(\sqrt{5}\)
y= \(2\sqrt{5}\)