Giúp mình câu này với
Rút gọn A=x20+25x19+25x18+...+25x2+25x+1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
ND
2
6 tháng 7 2021
\(\sqrt{36x^4\left(b-2\right)}^2=6x^2\left(2-b\right)=12x^2-6x^2b\)
6 tháng 7 2021
\(\sqrt{36x^4\left(b-2\right)^2}=6x^2\left|b-2\right|=6x^2\left(2-b\right)\) (vì b<2 nên b-2<0)
29 tháng 8 2021
a: Ta có: \(25x^2\left(x-y\right)-x+y\)
\(=\left(x-y\right)\left(25x^2-1\right)\)
\(=\left(x-y\right)\left(5x-1\right)\left(5x+1\right)\)
b: Ta có: \(16x^2\left(z^2-y^2\right)-z^2+y^2\)
\(=\left(z^2-y^2\right)\left(16x^2-1\right)\)
\(=\left(z-y\right)\left(z+y\right)\left(4x-1\right)\left(4x+1\right)\)
c: Ta có: \(x^3+x^2y-x^2z-xyz\)
\(=x^2\left(x+y\right)-xz\left(x+y\right)\)
\(=x\left(x+y\right)\left(x-z\right)\)
TD
1
AH
Akai Haruma
Giáo viên
6 tháng 11 2023
Lời giải:
$M=(x^{10}-24x^9)-(x^9-24x^8)+(x^8-24x^7)-(x^7-24x^6)+(x^6-24x^5)-(x^5-24x^4)+(x^4-24x^3)-(x^3-24x^2)+(x^2-24x)-(x-24)+1$
$=x^9(x-24)-x^8(x-24)+x^7(x-24)-.....+x(x-24)-(x-24)+1$
$=(x-24)(x^9-x^8+x^7-...+x-1)+1$
$=0.(x^9-x^8+....+x-1)+1=1$
TD
2
24 tháng 8 2023
\(M=x^{10}-25x^9+25x^8-25x^7+...-25x^3+25x^2-25x+25\)
Ta thấy : \(x=24\Rightarrow x+1=25\)
\(\Rightarrow M=x^{10}-\left(x+1\right)x^9+\left(x+1\right)x^8-\left(x+1\right)x^7+...-\left(x+1\right)x^3+\left(x+1\right)x^2-\left(x+1\right)x+\left(x+1\right)\)
\(M=x^{10}-x^{10}-x^9+x^9+x^8-x^8-x^7+...-x^4-x^3+x^3+x^2-x^2-x+x+1\)
\(\Rightarrow M=1\)
Vậy \(M=1\left(tạix=24\right)\)
18 tháng 10 2024
M=x
10
−25x
9
+25x
8
−25x
7
+...−25x
3
+25x
2
−25x+25
Ta thấy :
x
=
24
⇒
x
+
1
=
25
x=24⇒x+1=25
⇒
M
=
x
10
−
(
x
+
1
)
x
9
+
(
x
+
1
)
x
8
−
(
x
+
1
)
x
7
+
.
.
.
−
(
x
+
1
)
x
3
+
(
x
+
1
)
x
2
−
(
x
+
1
)
x
+
(
x
+
1
)
⇒M=x
10
−(x+1)x
9
+(x+1)x
8
−(x+1)x
7
+...−(x+1)x
3
+(x+1)x
2
−(x+1)x+(x+1)
M
=
x
10
−
x
10
−
x
9
+
x
9
+
x
8
−
x
8
−
x
7
+
.
.
.
−
x
4
−
x
3
+
x
3
+
x
2
−
x
2
−
x
+
x
+
1
M=x
10
−x
10
−x
9
+x
9
+x
8
−x
8
−x
7
+...−x
4
−x
3
+x
3
+x
2
−x
2
−x+x+1
⇒
M
=
1
⇒M=1
Vậy
M
=
1
(
t
ạ
i
x
=
24
)
M=1(tạix=24)
MA
17 tháng 9 2016
\(2-25x^2=0\)
\(\Rightarrow25x^2=2\)
\(\Rightarrow x^2=\frac{2}{25}\)
\(\Rightarrow x=\frac{\sqrt{2}}{5}\)
tíc mình nha
MA
17 tháng 9 2016
\(2-25x^2=0\)
\(\Leftrightarrow\left(\sqrt{2}-5x\right)\left(\sqrt{2}+5x\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}\sqrt{2}-5x=0\\\sqrt{2}+5x=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=\frac{\sqrt{2}}{5}\\x=-\frac{\sqrt{2}}{5}\end{cases}}\)
Vậy: \(x=\orbr{\begin{cases}x=\frac{\sqrt{2}}{5}\\x=-\frac{\sqrt{2}}{5}\end{cases}}\)
b) \(x^2-x+\frac{1}{4}=0\)
\(\Leftrightarrow\left(x-\frac{1}{2}\right)^2=0\)
\(\Leftrightarrow x-\frac{1}{2}=0\)
\(\Leftrightarrow x=\frac{1}{2}\)
13 tháng 3 2022
cảm ơn bạn nhưng bạn trình bày giúp mình được ko ạ mình cảm ơn:3
CM
10 tháng 1 2018
Biểu thức x 2 - 25 x 2 - 10 x + 25 x xác định khi x 0 và x ≠ 5.
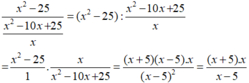
Ta có: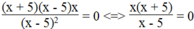 
khi x(x + 5) = 0 và x – 5
≠
0
x(x + 5) = 0 ⇔ x = 0 hoặc x + 5 = 0 ⇔ x = - 5
x = 0 không thỏa mãn điều kiện.
Vậy x = - 5 thì biểu thức x 2 - 25 x 2 - 10 x + 25 x có giá trị bằng 0.