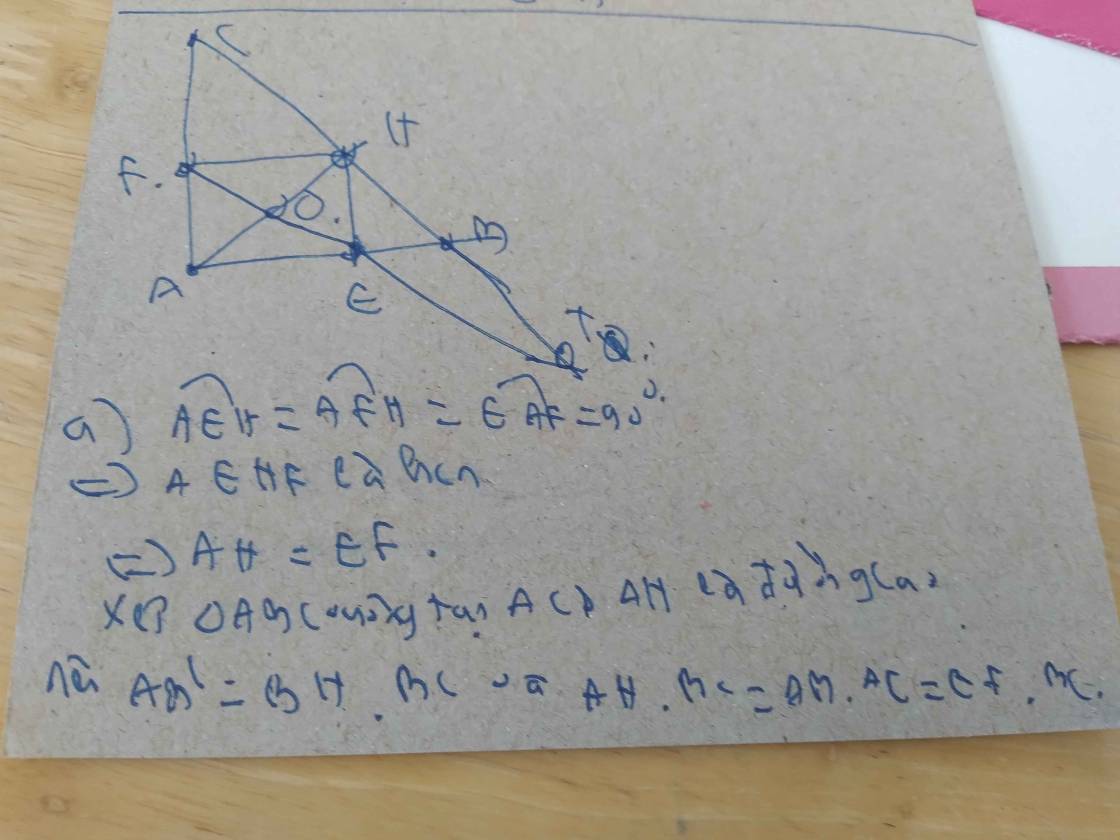
tam giác ABC vuông tại A có AB>AC đường cao AH, E và F theo thứ tự là hình chiếu vuông góc của H trên AB, AC. EF cắt AH tại O
a) chứng minh AB2=BH.BC và EF.BC= AB.AC
b) Gọi I, K lần lượt là trung điểm của HC, HB. Chứng minh\(\frac{1}{OH^2}=\frac{1}{OK^2}+\frac{1}{OI^2}\)
c) EF cắt BC tại T. Chứng minh TF.TE=TC.TB
c) ÈF