Giải giúp câu 38 với ạ 
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 35.
\(\xi_b=\xi=9V\)
\(r_b=\dfrac{r}{n}=\dfrac{r}{2}=\dfrac{2}{2}=1\Omega\)
\(R_Đ=\dfrac{U^2_Đ}{P_Đ}=\dfrac{3^2}{3}=3\Omega\)
\(R_{tđ}=\dfrac{R_1\cdot R_2}{R_1+R_2}+R_Đ=\dfrac{10\cdot10}{10+10}+3=8\Omega\)
Chọn A.
Câu 36.
\(I_Đ=I_m=\dfrac{\xi_b}{r_b+R_{tđ}}=\dfrac{9}{1+8}=1A\)
\(I_{Đđm}=\dfrac{P_Đ}{U_Đ}=\dfrac{3}{3}=1A\)
Vậy đèn sáng bình thường.
Chọn B
Câu 37.
\(U_2=U_{12}=I_{12}\cdot R_{12}=I\cdot R_{12}=1\cdot5=5V\)
\(I_2=\dfrac{U_2}{R_2}=\dfrac{5}{10}=0,5A\)
\(Q_{R_2tỏa}=R_2\cdot I_2^2t=10\cdot0,5^2\cdot2\cdot60=300J\)
Không có đáp án!!!
Câu 38.
Công suất trên toàn mạch:
\(P=\xi\cdot I=9\cdot1=9W\)
Điện năng sản ra trong toàn mạch 5 phút:
\(A=P\cdot t=9\cdot5\cdot60=2700J\)
Chọn C.
Câu 40.
Hiệu suát nguồn:
\(H=\dfrac{R_{tđ}}{r+R_{td}}=\dfrac{8}{1+8}=88,89\%\approx89\%\)
Chọn B


mình làm vài câu cho bạn tham khảo,các câu còn lại thì bạn làm tương tự thôi
23.\(\sqrt{14-2\sqrt{33}}=\sqrt{\left(\sqrt{11}\right)^2-2.\sqrt{11}.\sqrt{3}+\left(\sqrt{3}\right)^2}\)
\(=\sqrt{\left(\sqrt{11}-\sqrt{3}\right)^2}=\left|\sqrt{11}-\sqrt{3}\right|=\sqrt{11}-\sqrt{3}\)
28. \(\sqrt{25-4\sqrt{6}}=\sqrt{\left(2\sqrt{6}\right)^2-2.2\sqrt{6}.1+1^2}=\sqrt{\left(2\sqrt{6}-1\right)^2}\)
\(=\left|2\sqrt{6}-1\right|=2\sqrt{6}-1\)
29.\(\sqrt{14-8\sqrt{3}}=\sqrt{14-2\sqrt{48}}=\sqrt{\left(\sqrt{8}\right)^2-2\sqrt{6}.\sqrt{8}+\left(\sqrt{6}\right)^2}\)
\(=\sqrt{\left(\sqrt{8}-\sqrt{6}\right)^2}=\left|\sqrt{8}-\sqrt{6}\right|=\sqrt{8}-\sqrt{6}\)


38.
\(y'=2x^2-8x+9=2\left(x-2\right)^2+1\ge1\)
\(\Rightarrow\) Tiếp tuyến có hệ số góc nhỏ nhất bằng 1 khi \(x_0-2=0\Rightarrow x_0=2\)
\(y\left(2\right)=-\dfrac{11}{3}\)
Phương trình d:
\(y=1\left(x-2\right)-\dfrac{11}{3}=x-\dfrac{17}{3}\)
Thay tọa độ 4 điểm của đáp án, chỉ có \(P\left(5;-\dfrac{2}{3}\right)\) thỏa mãn
39.
Gọi E là trung điểm AB, F là trung điểm CD
Từ E kẻ EH vuông góc SF (H thuộc SF)
Do tam giác SAB đều \(\Rightarrow SE\perp AB\Rightarrow SE\perp\left(ABCD\right)\)
\(\Rightarrow SE\perp CD\)
\(EF||AD\Rightarrow EF\perp CD\)
\(\Rightarrow CD\perp\left(SEF\right)\) \(\Rightarrow CD\perp EH\)
\(\Rightarrow EH\perp\left(SCD\right)\Rightarrow EH=d\left(E;\left(SCD\right)\right)\)
Lai có: \(AB||CD\Rightarrow AB||\left(SCD\right)\Rightarrow d\left(A;\left(SCD\right)\right)=d\left(E;\left(SCD\right)\right)=EH\)
\(SE=\dfrac{AB\sqrt{3}}{2}=\dfrac{\sqrt{3}}{2}\) ; \(EF=AD=1\)
Hệ thức lượng: \(d=HE=\dfrac{SE.EF}{\sqrt{SE^2+EF^2}}=\dfrac{\sqrt{21}}{7}\)

Ủa hình như em hỏi rồi mà, ở dưới link này:
giúp em với - Hoc24


38:
a: (SAB) và (SAC) cùng vuông góc (ABC)
(SAB) cắt (SAC)=SA
=>SA vuông góc (ABC)
b: SA vuông góc CH
CH vuông góc AB
=>CH vuông góc (SAB)
=>(SCH) vuông góc (SAB)






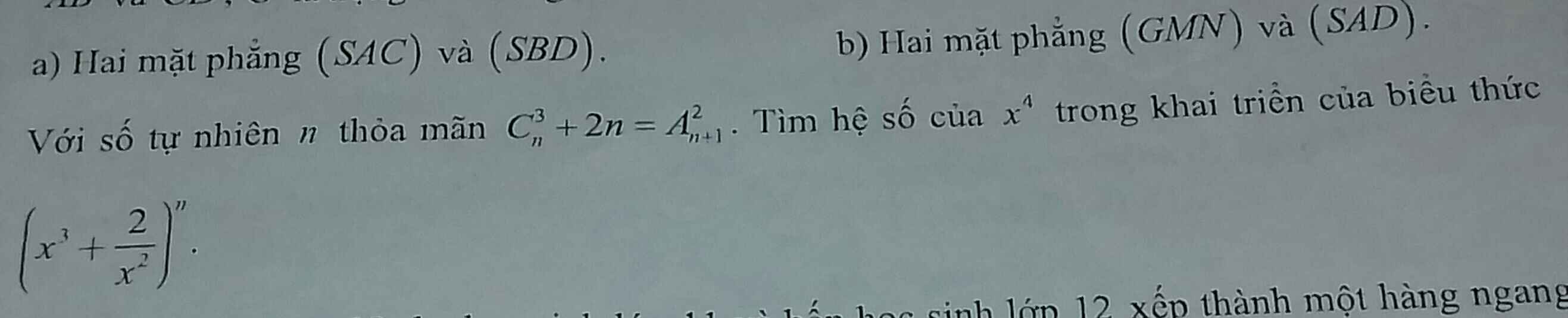



\(\dfrac{2x^2+x-3}{x^2-4}-2\le0\Leftrightarrow\dfrac{x+5}{x^2-4}\le0\)
\(\Leftrightarrow\dfrac{x+5}{\left(x-2\right)\left(x+2\right)}\le0\)
Bảng xét dấu:
Từ bảng xét dấu ta được nghiệm của BPT là:
\(\left[{}\begin{matrix}x\le-5\\-2< x< 2\end{matrix}\right.\)