3x=0 x=0 thì kết luận pt ntn vậy mng 😭
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 3 2022
bạn cứ ghi là:
Vậy phương trình có tập nghiệm: S={0}
hoặc
Vậy phương trình có nghiệm: x = 0
13 tháng 3 2022
bỏ cái x=0 đi
0x=1(vô lý)
xong kết luận là : vậy phương trình vô nghiệm
TD
4
CT
3
A
21 tháng 5 2019
0x=0
=> Phương trình đã cho có vô số nghiệm S={ x thuộc R }
hoặc Phương trình đã cho đúng với mọi x
21 tháng 5 2019
Kết luận:
Phương trình 0x = 0 có vô số nghiệm
Phương trình có tập nghiệm là: S = \(\left\{x\in R\right\}\)
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 10 2019
\(\left(m+3\right)x^2+\left(3-3m\right)x+2m-6=0\)
\(a+b+c=m+3+3-3m+2m-6=0\)
Phương trình luôn có 2 nghiệm: \(\left\{{}\begin{matrix}x_1=1\\x_2=\frac{2m-6}{m+3}\end{matrix}\right.\)
ML
1
M
9 tháng 4 2022
c,\(\dfrac{5-x}{2}-\dfrac{3x+4}{3}=\dfrac{1}{4}\)
⇔\(\dfrac{5-x}{2}+\dfrac{-3x-4}{3}=\dfrac{1}{4}\)
⇔\(\dfrac{6\left(5-x\right)}{12}+\dfrac{4\left(-3x-4\right)}{12}=\dfrac{3}{12}\)
⇔6(5-x)+4(-3x-4)=3
⇔ 30-6x-12x-16=3
⇔ 30-16-3=12x+6x
⇔ 11=18x
⇔ x=\(\dfrac{11}{18}\)
Vậy S=\(\left\{\dfrac{11}{18}\right\}\)
d)x2-5x=9(x-5)
⇔x(x-5)=9(x-5)
⇔x(x-5)-9(x-5)=0
⇔(x-9)(x-5)=0
⇔\(\left\{{}\begin{matrix}x-9=0\Leftrightarrow x=9\\x-5=0\Leftrightarrow x=5\end{matrix}\right.\)
Vậy S=\(\left\{5;9\right\}\)
1 tháng 6 2022
a: \(\Leftrightarrow\left(4x+12\right)\left(3x-2\right)-\left(3x+3\right)\left(4x-1\right)=-27\)
\(\Leftrightarrow12x^2-8x+36x-24-\left(12x^2-3x+12x-3\right)=-27\)
\(\Leftrightarrow12x^2+28x-24-12x^2-9x+3=-27\)
\(\Leftrightarrow19x-21=-27\)
=>19x=-6
hay x=-6/19
b: \(\left(x+1\right)\left(3x^2-x+1\right)+x^2\left(4-3x\right)=\dfrac{5}{2}\)
\(\Leftrightarrow3x^3-x^2+x+3x^2-x+1+4x^2-3x^3=\dfrac{5}{2}\)
\(\Leftrightarrow6x^2+1=\dfrac{5}{2}\)
\(\Leftrightarrow6x^2=\dfrac{3}{2}\)
\(\Leftrightarrow x^2=\dfrac{3}{12}=\dfrac{1}{4}\)
=>x=1/2 hoặc x=-1/2
c: \(\Leftrightarrow2\left(x^2-4\right)-4\left(x^2-x-2\right)+\left(5x+8\right)\left(x+2\right)=0\)
\(\Leftrightarrow2x^2-8-4x^2+4x+8+5x^2+10x+8x+16=0\)
\(\Leftrightarrow3x^2+22x+16=0\)
\(\text{Δ}=22^2-4\cdot3\cdot16=292>0\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{-22-2\sqrt{73}}{6}=\dfrac{-11-\sqrt{73}}{3}\\x_2=\dfrac{-11+\sqrt{73}}{3}\end{matrix}\right.\)
d: \(\Leftrightarrow20x^2-16x-1=10x^2-2x+5x-1\)
\(\Leftrightarrow10x^2-19x=0\)
=>x(10x-19)=0
=>x=0 hoặc x=19/10
30 tháng 4 2022
a=1; b=-2m-2; c=-4
Vì ac<0
nên phương trình luôn có hai nghiệm phân biệt
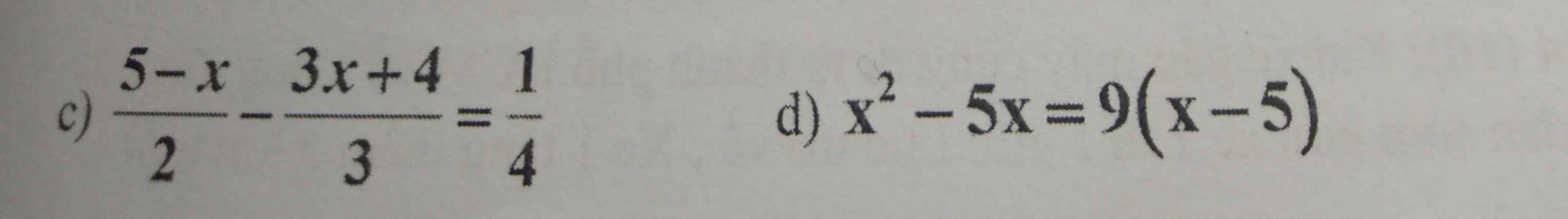
Vậy \(S=\left\{0\right\}\)