CMR: Khoảng cách từ một đỉnh tới trực tâm của một tam giác bằng \(\frac{1}{2}\) lần khoảng cách từ tâm đường tròn ngoại tiếp tam giác đó đến cạnh nối hai đỉnh còn lại.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



O là tâm đường tròn ngoại tiếp tam giác ABC nên ta vẽ đường kính AOE
Tứ giác BHCE là hình bình hành
M là trung điểm của BC. Do đó M là trung điểm của HE.
Kết hợp với O là trung điểm của AE suy ra OM là đường trung bình của \(\Delta AHE\)
\(\Rightarrow OM=\frac{1}{2}AH\)hay 2OM = AH
Vậy khoảng cách từ trực tâm tới đỉnh bằng 2 lần khoảng cách từ giao điểm các đường trung trực tới cạnh đối diện đỉnh đó (đpcm)

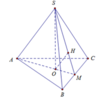
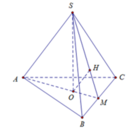
Đáp án A
Ta có O M = 1 3 A M = a 3 3
Lại có d O ; S B C = O H = a 2 ⇒ S O = a
Mặt khác R N = O A = 2 a 3 3 ; h = S O = a ⇒ V = 1 3 π R 2 h = 4 π a 3 9

Câu hỏi của marivan2016 - Toán lớp 9 - Học toán với OnlineMath
Tham khảo nha!
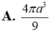
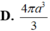
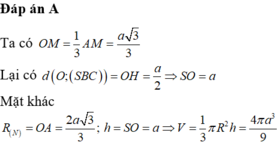
SÔNG CÓ KHÚC NGƯỜI CÓ LÚC MÀ BẠN .
TRÁCH BẠN ẤY LÀM GÌ
ối trời ơi đến cả zZz Phan Cả Phát zZz cũng phải đi hỏi bài ư?
Thế mà gọi là thần đồng
~~~~