Cho cosα=\(\dfrac{1}{3}\) với 0<α<\(\dfrac{\pi}{2}\).Tính các giá trị lượng giác còn lại của góc α.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Với 0 < α < π/2 thì cosα >0, sinα >0. Ta có
1 - sin 2 α = cos 2 α
Mặt khác cos 2 α = ( 2 sin α ) 2 = 4 sin 2 α nên 5 sin 2 α = 1 hay
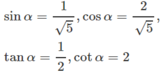

a: pi/2<a<pi
=>sin a>0
\(sina=\sqrt{1-\left(-\dfrac{1}{\sqrt{3}}\right)^2}=\dfrac{\sqrt{2}}{\sqrt{3}}\)
\(sin\left(a+\dfrac{pi}{6}\right)=sina\cdot cos\left(\dfrac{pi}{6}\right)+sin\left(\dfrac{pi}{6}\right)\cdot cosa\)
\(=\dfrac{\sqrt{3}}{2}\cdot\dfrac{\sqrt{2}}{\sqrt{3}}+\dfrac{1}{2}\cdot-\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{6}-2}{2\sqrt{3}}\)
b: \(cos\left(a+\dfrac{pi}{6}\right)=cosa\cdot cos\left(\dfrac{pi}{6}\right)-sina\cdot sin\left(\dfrac{pi}{6}\right)\)
\(=\dfrac{-1}{\sqrt{3}}\cdot\dfrac{\sqrt{3}}{2}-\dfrac{\sqrt{2}}{\sqrt{3}}\cdot\dfrac{1}{2}=\dfrac{-\sqrt{3}-\sqrt{2}}{2\sqrt{3}}\)
c: \(sin\left(a-\dfrac{pi}{3}\right)\)
\(=sina\cdot cos\left(\dfrac{pi}{3}\right)-cosa\cdot sin\left(\dfrac{pi}{3}\right)\)
\(=\dfrac{\sqrt{2}}{\sqrt{3}}\cdot\dfrac{1}{2}+\dfrac{1}{\sqrt{3}}\cdot\dfrac{\sqrt{3}}{2}=\dfrac{\sqrt{2}+\sqrt{3}}{2\sqrt{3}}\)
d: \(cos\left(a-\dfrac{pi}{6}\right)\)
\(=cosa\cdot cos\left(\dfrac{pi}{6}\right)+sina\cdot sin\left(\dfrac{pi}{6}\right)\)
\(=\dfrac{-1}{\sqrt{3}}\cdot\dfrac{\sqrt{3}}{2}+\dfrac{\sqrt{2}}{\sqrt{3}}\cdot\dfrac{1}{2}=\dfrac{-\sqrt{3}+\sqrt{2}}{2\sqrt{3}}\)

$\sin \alpha =2$?? $\sin \alpha \in [-1;1]$ với mọi $\alpha$ mà bạn. Bạn xem lại đề.

\(\sin^2x=\sqrt{1-\left(-\dfrac{4}{5}\right)^2}=\dfrac{9}{25}\)
mà \(\sin x>0\)
nên \(\sin x=\dfrac{3}{5}\)
=>\(\tan x=-\dfrac{3}{4}\)
\(\Leftrightarrow\cot x=-\dfrac{4}{3}\)

\(\dfrac{\pi}{2}< x< \pi\Rightarrow cosx< 0\)
\(\Rightarrow cosx=-\sqrt{1-sin^2x}=-\dfrac{20}{29}\)
\(tanx=\dfrac{sinx}{cosx}=-\dfrac{21}{20}\)
\(cotx=\dfrac{1}{tanx}=-\dfrac{20}{21}\)

a.Ta có : \(x\in\left(\pi;\dfrac{3}{2}\pi\right)\Rightarrow cosx< 0\)
\(cosx=-\sqrt{1-sin^2x}=-\sqrt{1-0,8^2}=-0,6\)
\(tanx=\dfrac{4}{3};cotx=\dfrac{3}{4}\)
b. cos 2x = \(cos^2x-sin^2x=0,6^2-0,8^2=-0,28\)
\(P=2.cos2x=-0,56\)
\(Q=tan\left(2x+\dfrac{\pi}{3}\right)=\dfrac{tan2x+tan\dfrac{\pi}{3}}{1-tan2x.tan\dfrac{\pi}{3}}=\dfrac{tan2x+\sqrt{3}}{1-tan2x.\sqrt{3}}\)
tan 2x = \(\dfrac{2tanx}{1-tan^2x}=\dfrac{\dfrac{2.4}{3}}{1-\left(\dfrac{4}{3}\right)^2}=\dfrac{-24}{7}\)
\(Q=\dfrac{-\dfrac{24}{7}+\sqrt{3}}{1+\dfrac{24}{7}.\sqrt{3}}\) \(=\dfrac{-24+7\sqrt{3}}{7+24\sqrt{3}}\)

b)\(P=cos2a-cos(\dfrac{\pi}{3}-a) \\=2cos^2a-1-cos\dfrac{\pi}{3}cosa-sin\dfrac{\pi}{3}sina \\=2.(\dfrac{-2}{5})^2-1-\dfrac{1}{2}.\dfrac{-2}{5}-\dfrac{\sqrt3}{2}.\dfrac{-\sqrt{21}}{5} \\=\dfrac{-24+15\sqrt7}{50}\)
a, Vì : \(\pi< a< \dfrac{3\pi}{2}\) nên \(cos\alpha< 0\) mà \(cos^2\alpha=1-sin^2\alpha=1-\dfrac{4}{25}=\dfrac{21}{25},\)
do đó : \(cos\alpha=-\dfrac{\sqrt{21}}{5}\)
từ đó suy ra : \(tan\alpha=\dfrac{2}{\sqrt{21}},cot\alpha=\dfrac{\sqrt{21}}{2}\)

\(\cos^2x=\sqrt{1-\dfrac{9}{25}}=\dfrac{16}{25}\)
mà \(\cos x< 0\)
nên \(\cos x=-\dfrac{4}{5}\)
=>\(\tan x=-\dfrac{3}{4};\cot x=-\dfrac{4}{3}\)

Em 2k8 ms học nên k chắc
Vì 0 < \(\alpha< \dfrac{\pi}{2}\) => sin \(\alpha>0\)
Cos \(\alpha=\dfrac{1}{3}\) \(\Rightarrow sin\alpha=\sqrt{1-\dfrac{1}{9}}=\dfrac{2\sqrt{2}}{3}\)
tan \(\alpha=2\sqrt{2}\) ; cot \(\alpha=\dfrac{1}{2\sqrt{2}}\)
giỏi v em lm đúng r đấy