Cho tam giác ABC 3 góc nhọn.AB=c,AC=b.BC=a.Cm: a/sinA =b/sinB =c/sinC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 8 2019
Tự vẽ hình
Kẻ BH \(\perp\)AC và \(CK\perp\)AB
Tam giác AKC vuông tại K
=>CK=bsinA (1)
Tam giác BKC vuông tại K
=>CK=asinB (2)
Từ (1) (2)=>bsinA=asinB
<=>\(\frac{a}{sinA}=\frac{b}{sinB}\)
Chứng minh tương tự ta có :\(\frac{a}{sinA}=\frac{c}{sinC}\)
Vậy ....
ND
1
4 tháng 8 2023
Kẻ AH vuông góc BC
Xét ΔAHB vuông tại H có sin B=AH/AB
=>AH=c*sin B
Xét ΔAHC vuông tại H có sin C=AH/AC
=>AH=AC*sin C=b*sin C
=>c*sin B=b*sin C
=>c/sinC=b/sinB
Kẻ BK vuông góc AC
Xét ΔABK vuông tại K có
sin A=BK/AB
=>BK=c*sinA
Xét ΔBKC vuông tại K có
sin C=BK/BC
=>BK/a=sin C
=>BK=a*sin C
=>c*sin A=a*sin C
=>c/sin C=a/sin A
=>a/sin A=b/sinB=c/sinC
NT
0
CM
7 tháng 9 2019
ta có
sinA + sinB – sinC = 4sin (A/2) sin(B/2) cos(C/2) (2)
suy ra điều phải chứng minh.
P
2
28 tháng 6 2021
Ta có : \(S_{ABC}=\dfrac{1}{2}bc.sinA=\dfrac{1}{2}acSinB=\dfrac{1}{2}abSinC\)
\(\Rightarrow bc.sinA=acSinB=abSinC\)
- Lấy abc chia cho cả 3 vế ta được ĐPCM
28 tháng 6 2021
Kẻ AH⊥BC
Xét ΔABH vuông tại H có \(AH=c\cdot\sin\widehat{B}\)
Xét ΔACH vuông tại H có \(AH=b\cdot\sin\widehat{C}\)
\(\Leftrightarrow\left\{{}\begin{matrix}c=\dfrac{AH}{\sin\widehat{B}}\\b=\dfrac{AH}{\sin\widehat{C}}\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}\sin\widehat{B}=\dfrac{AH}{c}\\\sin\widehat{C}=\dfrac{AH}{b}\end{matrix}\right.\Leftrightarrow\dfrac{c}{\sin\widehat{C}}=\dfrac{b}{\sin\widehat{B}}\)(1)
Kẻ BK⊥AC
Cm tương tự, ta được: \(\dfrac{a}{\sin\widehat{A}}=\dfrac{c}{\sin\widehat{C}}\)(2)
Từ (1), (2) suy ra đpcm
MH
16 tháng 3 2021
Lời giải:
a) Theo định lý sin và áp dụng tính chất dãy tỉ số bằng nhau ta có:
asinA=bsinB=csinC=b+csinB+sinC=2asinB+sinCasinA=bsinB=csinC=b+csinB+sinC=2asinB+sinC
⇒1sinA=2sinB+sinC⇒1sinA=2sinB+sinC
⇒2sinA=sinB+sinC⇒2sinA=sinB+sinC (đpcm)
b) Theo định lý sin ta có:
asinA=bsinB=csinCasinA=bsinB=csinC
⇒(asinA)2=bsinB.csinC=a2sinB.sinC⇒(asinA)2=bsinB.csinC=a2sinB.sinC
⇒sin2A=sinB.sinC⇒sin2A=sinB.sinC (đpcm)
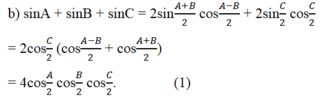
Kẻ đường cao : BH , AI , CK
Ta có: sinA = BH / c ; sinB = AI / c
=> sinA/sinB = BH / AI (1)
Mà BH = a.sinC ; AI = b.sinC
=> BH/AI = a/b (2)
Từ (1) và (2) suy ra sinA/sinB = a/b => a/sinA = b/sinB
Bạn chỉ việc nói chứng minh tượng tự , ta có:
b/sinB = c/sinC ; c/sinC = a/sinA
Từ đó suy ra a /sinA = b / sinB = c /sinC
Chúc bạn học tốt
Tự vẽ hình
Kẻ BH \(\perp\)AC và \(CK\perp\)AB
Tam giác AKC vuông tại K
=>CK=bsinA (1)
Tam giác BKC vuông tại K
=>CK=asinB (2)
Từ (1) (2)=>bsinA=asinB
<=>\(\frac{a}{sinA}=\frac{b}{sinB}\)
Chứng minh tương tự ta có :\(\frac{a}{sinA}=\frac{c}{sinC}\)
Vậy ....