Tìm GTNN
M = x2 + y2 - x + 6y +10
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
4 tháng 12 2018
Ta có: M = x 2 + y 2 – x + 6y + 10 = ( y 2 + 6y + 9) + ( x 2 – x + 1)
= y + 3 2 + ( x 2 – 2.1/2 x + 1/4) + 3/4 = y + 3 2 + x - 1 / 2 2 + 3/4
Vì y + 3 2 ≥ 0 và x - 1 / 2 2 ≥ 0 nên y + 3 2 + x - 1 / 2 2 ≥ 0
⇒ M = y + 3 2 + x - 1 / 2 2 + 3/4 ≥ 3/4
⇒ M = 3/4 khi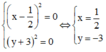 
Vậy M = 3/4 là giá trị nhỏ nhất tại y = -3 và x = 1/2
12 tháng 7 2018
a, (x^2 -2x+1)+(y^2 +6y+9) =0
(x-1)^2 +(y+3)^2 =0
Do đó: x-1=0 và y+3=0
Vậy x=1 và y=-3
b, x^2 +y^2 +1=xy+x+y
2x^2 +2y^2 +2=2xy+2x+2y
2x^2 +2y^2 -2xy-2x-2y +2=0
(x^2 -2x+1)+(y^2 -2y+1)+ (x^2 +y^2 -2xy)=0
(x-1)^2 +(y-1)^2 +(x-y)^2 =0
Suy ra: x-1=0, y-1=0 và x-y=0
Vậy x=1,y=1
c,5x^2 - 4x-2xy+y^2 +1=0
(4x^2 -4x+1)+(x^2 -2xy+y^2 )=0
(2x-1)^2 +(x-y)^2 =0
Do đó: 2x-1 =0 và x=y suy ra: x=0,5 và x=y
Vậy x=y=0,5
23 tháng 10 2021
a: ta có: \(P=x^2+10x+27\)
\(=x^2+10x+25+2\)
\(=\left(x+5\right)^2+2\ge2\forall x\)
Dấu '=' xảy ra khi x=-5
21 tháng 9 2021
\(a,P=x^2-2x+5=\left(x^2-2x+1\right)+4=\left(x-1\right)^2+4\ge4\)
Dấu \("="\Leftrightarrow x=1\)
\(b,Q=2x^2-6x=2\left(x^2-2\cdot\dfrac{3}{2}x+\dfrac{9}{4}-\dfrac{9}{4}\right)=2\left(x-\dfrac{3}{2}\right)^2-\dfrac{9}{2}\ge-\dfrac{9}{2}\)
Dấu \("="\Leftrightarrow x=\dfrac{3}{2}\)
\(c,M=\left(x^2-x+\dfrac{1}{4}\right)+\left(y^2+6y+9\right)+\dfrac{3}{4}=\left(x-\dfrac{1}{2}\right)^2+\left(y+3\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\)
Dấu \("="\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=-3\end{matrix}\right.\)
21 tháng 9 2021
a: Ta có: \(P=x^2-2x+5\)
\(=x^2-2x+1+4\)
\(=\left(x-1\right)^2+4\ge4\forall x\)
Dấu '=' xảy ra khi x=1
TC
2
9 tháng 8 2016
a) \(P=x^2-2x+5\)
\(=x^2-2x+1+4\)
\(=\left(x-1\right)^2+4\ge4\)
\(MinP=4\Leftrightarrow x-1=0\Rightarrow x=1\)
b) \(Q=2x^2-6x\)
\(=2\left(x^2-3x\right)\)
\(=2\left(x^2-2.x.\frac{3}{2}+\frac{9}{4}-\frac{9}{4}\right)\)
\(=2\left(\left(x-\frac{3}{2}\right)^2-\frac{9}{4}\right)\)
\(=-\frac{9}{2}-2\left(x-\frac{3}{2}\right)^2\le\frac{-9}{2}\)
\(MinQ=\frac{-9}{2}\Leftrightarrow x-\frac{3}{2}=0\Rightarrow x=\frac{3}{2}\)
9 tháng 8 2016
M=x^2+y^2-x+6y+10
M=(x^2-x+1/4)+(y^2+6y+9)+3/4
M=(x-1/2)^2+(y+3)^2+3/4
\(minM=\frac{3}{4}\Leftrightarrow\hept{\begin{cases}x=\frac{1}{2}\\y=-3\end{cases}}\)
CM
22 tháng 2 2019
Chọn B.
Phương pháp:
Biến đổi đẳng thức đã cho để đưa về dạng phương trình đường tròn (C) tâm I bán kính R.
Từ đó ta đưa bài toán về dạng bài tìm M x ; y ∈ C để O M - a lớn nhất hoặc nhỏ nhất.
Xét các trường hợp xảy ra để tìm a.
Cách giải:
NT
2
1 tháng 3 2022
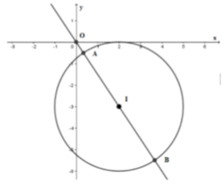
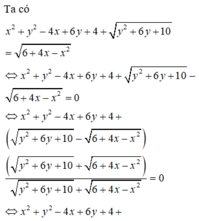
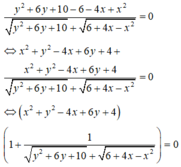
\(x^2-4x+y^2-6y+15=2\)
\(\Leftrightarrow\left(x^2-4x+4\right)+\left(y^2-9y+9\right)+2=2\)
\(\Leftrightarrow\left(x-2\right)^2+\left(y-3\right)^2=0\)
Vì \(\left(x-2\right)^2\ge0;\left(y-3\right)^2\ge0\)
Mà \(\left(x-2\right)^2+\left(y-3\right)^2=0\)
\(\Rightarrow\left\{{}\begin{matrix}\left(x-2\right)^2=0\\\left(y-3\right)^2=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=3\end{matrix}\right.\)
Vậy (x;y) = (2;3)
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 3 2022
\(\Leftrightarrow\left(x^2-4x+4\right)+\left(y^2-6y+9\right)=0\)
\(\Leftrightarrow\left(x-2\right)^2+\left(y-3\right)^2=0\)
Do \(\left\{{}\begin{matrix}\left(x-2\right)^2\ge0\\\left(y-3\right)^2\ge0\end{matrix}\right.\) ;\(\forall x;y\Rightarrow\left(x-2\right)^2+\left(y-3\right)^2\ge0\)
Đẳng thức xảy ra khi và chỉ khi:
\(\left\{{}\begin{matrix}x-2=0\\y-3=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=2\\y=3\end{matrix}\right.\)
CM
5 tháng 11 2017
a) Cách 1.
Ta có 2xy + 3z + 6y + xz = (2xy + xz) + (3z + 6y)
= x(2 y + z)+3(z + 2 y) = (z + 2y)(x + 3).
Cách 2.
Ta có 2xy + 3z + 6y + xz = (2x1/ + 6y) + (3z + xz)
= 2y(x + 3) + z(3 + x) = (z + 2y)(x + 3).
b) Biến đổi được a 4 - 9 rt 3 + a 2 -9a = (a- 9)a( a 2 +1).
c) Biến đổi được 3 x 2 + 5y - 3xy + (-5x) = (x - y)(3x - 5).
d) Biến đổi được x 2 - (a + b)x + ab = (x- a)(x - b).
e) Ta có 4 x 2 - 4xy + y 2 – 9 t 2 = ( 2 x - y ) 2 - ( 3 t ) 2
= (2x - y - 3t )(2x - y + 31).
g) Ta có x 3 - 3 x 2 y + 3 xy 2 - y 3 - z 3
= ( x - y ) 3 - z 3 = (x - y - z)( x 2 + y 2 + z 2 - 2xy + xz - yz).
h) Ta có x 2 - y 2 + 8x + 6y+ 7 = ( x 2 +8x + 16) - ( y 2 - 6y+ 9)
= ( x + 4 ) 2 - ( y - 3 ) 2 =(x-y + 7)(x + y + l).
17 tháng 6 2021
\(a,-x^2+2x+5=-\left(x^2-2x-5\right)=-\left(x^2-2x+1-6\right)=-\left(x-1\right)^2+6\le6\)
dấu'=' xảy ra<=>x=1=>Max A=6
\(b,B=-x^2-y^2+4x+4y+2=-x^2+4x-4-y^2+4x-4+10\)
\(=-\left(x^2-4x+4\right)-\left(y^2-4x+4\right)+10\)
\(=-\left(x-2\right)^2-\left(y-2\right)^2+10=-\left[\left(x-2\right)^2+\left(y-2\right)^2\right]+10\le10\)
dấu"=" xảy ra<=>x=y=2=>Max B=10
\(c,C=x^2+y^2-2x+6y+12=\left(x-1\right)^2+\left(y+3\right)^2+2\ge2\)
dấu'=' xảy ra<=>x=1,y=-3=>MinC=2
Ta có :
\(M=x^2+y^2-x+6y+10\)
\(=\left(x^2-x+\frac{1}{4}\right)+\left(y^2+6y+9\right)+\frac{3}{4}\)
\(=\left(x-\frac{1}{2}\right)^2+\left(y+3\right)^2+\frac{3}{4}\ge\frac{3}{4}\)
\(\Rightarrow M_{min}=\frac{3}{4}\Leftrightarrow\hept{\begin{cases}x=\frac{1}{2}\\y=-3\end{cases}}\)
Vậy ...
\(M=x^2+y^2-x+6y+10\)
\(=\left(x^2-2.x\frac{1}{2}+\frac{1}{4}\right)+\left(y^2+6y+9\right)+10,75\)
\(=\left(x-\frac{1}{2}\right)^2+\left(x+3\right)^2+10,75\ge10,75\)
\(MinM=10,75\Leftrightarrow\hept{\begin{cases}x-\frac{1}{2}=0\\x+3=0\end{cases}\Rightarrow\hept{\begin{cases}x=\frac{1}{2}\\x=-3\end{cases}}}\)